Recap
Through a series of regression models, I tested the hypothesis that more and higher draft picks translated into wins on the field. It became clear that neither conventional draft points nor Massey-Thaler surplus values were significant predictors of team wins the following season when previous year wins were taken into account.
One important point: It goes without saying that what really matters is the players who are picked. The most over-cited example contrasts Tom Brady, picked in the 6th round, and Ryan Leaf, picked #2 overall. The same principle holds throughout the draft. What is truly important is how good the chosen players are, and not how high the pick was. However, on average, players picked higher definitively outperform players picked lower. Over time the significance of any one player outperforming or underperforming his place in the draft should average out. Theoretically, in a large enough sample, draft picks (not the players) should correlate with team talent levels and therefore wins too.
Are draft pick values non-significant because they don't matter, or because we don't have enough data? Consider M-T values in 2005 as a case study. The coefficient for M-T value without accounting for previous year's wins is 0.86 wins per million $ of surplus value. The coefficient drops to 0.24 when accounting for previous year's wins, but we cannot have much confidence in that number because it is not significant (p=0.42).
Example 1
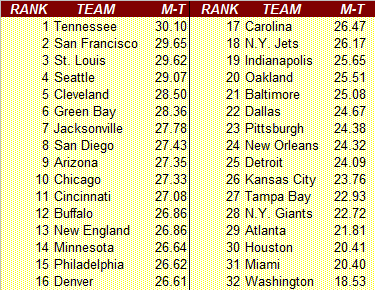
In 2005, the team with the most M-T value was TEN with $5.3 million in surplus. The team with the least M-T value was NYG with $2.2 million. (The average was $3.7 million.) That's a difference of $3.1 million between the top and bottom teams.
Using the 0.24 wins/$value coefficent, we get:
3.1 x 0.24 = 0.75 wins.
Between the top team and bottom team in terms of M-T draft value, we could estimate a difference of 0.75 wins. That's a very rough estimate because of the lack of statistical significance, but it is significant in NFL terms. 0.75 games would be a lot in a 16 game season.
Example 2
Let's do the same drill with conventional draft points in the same year, 2005. Without considering the previous year's record, the coefficient for draft points was 0.0022 wins/draft pt. The coefficient drops to 0.00040 when accounting for previous year's wins, but it is not signficant (p=0.36).
In 2005, the team with the most draft points was SF with 4049 and the team with the least was BUF with 603 for a difference of 3446. The average that year was 1898 points.
Using the 0.00040 wins/pt coefficient, we get:
0.00040 x 3446 = 1.37 wins.
1.37 wins is very significant in NFL terms in a 16-game season, especially considering that the difference between 9-7 and 7-9 sometimes means going to the playoffs or firing the head coach. We just can't have much confidence that the real number is 1.37 without more data.
ConclusionThis leads me to suspect that conventional draft points, M-T values, or other measures of draft "capital" are probably important to a team's fortunes. I simply don't have a database large enough (yet) to determine a significant coefficient. But in the case studies above give us an idea of the likely potential magnitude of the effects. Admittedly, it is possible that the effects are zero or near-zero (or even negative). There is a third possibility--that draft picks do matter, but neither conventional draft points nor M-T surplus are good measures of their value. Another system of values, one that is calibrated to the effect the picks have on wins, might prove to be the best method of valuing draft picks.
The effect of the previous year's wins is powerful. The constant churn of poor teams improving and good teams getting worse dominates the effect of either draft variable. Ignoring draft variables, teams with 3 wins tend to improve to 7 wins the following year. Teams with 12 wins one year tend to stumble to 9 wins the next. I suspect this is partially why it is difficult to distill the true effect on wins of draft picks, assuming there is one.
The reasons for the churn may include strength of schedule, salary cap considerations, and the draft. But luck and other mathematical reasons may also be at work. I plan to address this in a later post.

 I ran several more regressions and got very similar results to the conventional draft point models. Adding various combinations of M-T values, previous year values, and cumulative values did not improve the r-squared found by using last year's wins alone, which is about 0.37. Below is the table of results. Asterisks denote significance and negative coefficents are in red.
I ran several more regressions and got very similar results to the conventional draft point models. Adding various combinations of M-T values, previous year values, and cumulative values did not improve the r-squared found by using last year's wins alone, which is about 0.37. Below is the table of results. Asterisks denote significance and negative coefficents are in red.




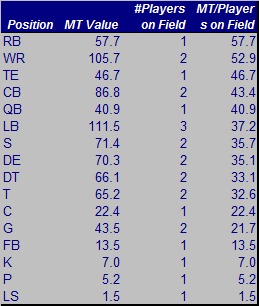



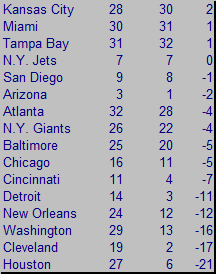 There are some exceptions, but we see generally successful teams at the top of the list and generally unsuccessful teams at the bottom. It's a rough analysis, but it leads me to believe there is some level of correlation between maneuvering for M-T surplus value and team success on the field. Keep in mind, bottom-feeder teams with the top picks have more M-T surplus value than winning teams with the later picks. Therefore, if there truly is a significant correlation between wins and M-T value, the direction of causation would be from M-T value to wins, not vice-versa.
There are some exceptions, but we see generally successful teams at the top of the list and generally unsuccessful teams at the bottom. It's a rough analysis, but it leads me to believe there is some level of correlation between maneuvering for M-T surplus value and team success on the field. Keep in mind, bottom-feeder teams with the top picks have more M-T surplus value than winning teams with the later picks. Therefore, if there truly is a significant correlation between wins and M-T value, the direction of causation would be from M-T value to wins, not vice-versa.
 One team does stand out at the top. Tennessee is certainly an outlier at the top of the list with a difference of 20. Admittedly, this is not a sophisticated statistical test. Ordinal rankings are rarely as powerful as proportional continuous values, but they are still very useful.
One team does stand out at the top. Tennessee is certainly an outlier at the top of the list with a difference of 20. Admittedly, this is not a sophisticated statistical test. Ordinal rankings are rarely as powerful as proportional continuous values, but they are still very useful.