 Previous research on the balance between running and passing in the NFL has largely missed the mark because it has focused on only half of the equation. Opposing defenses have been ignored. In this article, I'll illustrate how game theory can be applied to football play calling, and how it explains the balance between various strategies.
Previous research on the balance between running and passing in the NFL has largely missed the mark because it has focused on only half of the equation. Opposing defenses have been ignored. In this article, I'll illustrate how game theory can be applied to football play calling, and how it explains the balance between various strategies.
The research to date, notably the Alamar and Rockerbie papers along with my own articles, typically follow the same approach. They calculate the average expected yardage gain by running and by passing, accounting for various risks such as incompletions, turnovers, or sacks. The difference between the average expected gains for running and passing is then presented as a puzzle. If for example, passing yields a higher average gain than running, why don’t teams pass more often?
Further, if passing is far preferable to running, why should a team run at all? Hopefully that's obvious. An opposing defense could exclusively focus on defending the pass, dramatically limiting any expected gain.
 Yet the better play choice remains the pass. So I should pass more often than run, right? But the defense knows this too, so I know he'll certainly play a pass defense. Therefore, I should run. But he knows I know that he knows that...and around we go. This is where game theory comes in. Game theory can actually quantify the optimum mix of strategies mathematically.
Yet the better play choice remains the pass. So I should pass more often than run, right? But the defense knows this too, so I know he'll certainly play a pass defense. Therefore, I should run. But he knows I know that he knows that...and around we go. This is where game theory comes in. Game theory can actually quantify the optimum mix of strategies mathematically.
Offenses in the NFL do not consist of simple run or pass decisions. In reality there are a myriad of formations, plays, and variations available as options. Likewise, defenses have a similar number of alternatives. But for now, just to illustrate the potential for game theory to help understand play calling, let's limit offenses to two strategies: the run and the pass. Defenses are limited to three: run defense, pass defense, and the blitz.
The example below represents a single NFL play as a "game." The number in each cell is the offense's "utility" given the combination of offensive and defensive strategy employed. The utility is not necessarily the yardage gained or expected points, but simply a proportionate scale of how preferred an expected outcome is to the others. And since football is a zero-sum game, the defense's utility is always the negative of the offense's.
| Defense | ||||
| Run D | Pass D | Blitz | ||
| Offense | Run | -3 | 4 | 6 |
| Pass | 9 | -3 | -5 | |
For example, if the offense chooses a run play and the defense chooses a run defense, then the outcome would be "-3" to the offense. This doesn't mean the offense would always lose 3 yards on such a play, but that the outcome is typically a setback, say a gain of only 2 yards or less. The utility to the defense would be +3 because what's bad for the offense is equally good for the defense.
 In this example a run play against a pass defense yields a positive result of 4 units. A pass against a run defense yields an even larger payoff of 9. A blitz against a pass play could set the offense back by -5 units. But the blitz is risky because if the offense had called for a run, it would likely be fairly successful. Each strategy option for both the offense and defense has its advantages, disadvantages, and risks based on which strategy the opponent has chosen.
In this example a run play against a pass defense yields a positive result of 4 units. A pass against a run defense yields an even larger payoff of 9. A blitz against a pass play could set the offense back by -5 units. But the blitz is risky because if the offense had called for a run, it would likely be fairly successful. Each strategy option for both the offense and defense has its advantages, disadvantages, and risks based on which strategy the opponent has chosen.From the offense's point of view, it appears that running is the safer bet. Two of the three possible outcomes are positive, and the worst possible outcome is no worse than -3. Passing has the highest possible payoff, but two of the three outcomes are negative. There is no clear-cut "dominant" strategy choice for the offense.
The best approach is to unpredictably sometimes run and sometimes pass, which game theory calls a mixed strategy. This is also what we see in reality. In fact, game theory methods can actually "solve" the game, providing the optimum proportion of running and passing. The solution is what's known as a Nash equilibrium, named after the mathematician made famous by the movie A Beautiful Mind. The Nash equilibrium is the mix of strategies where each opponent, knowing the strategies of the other, has nothing to gain by changing his own strategy. In other words, an offense is choosing the best proportion of play calls taking into account the defense's strategy mix, and the defense is choosing its best proportion of strategies knowing the offense's strategy mix.
 On the football field, the equilibrium point is found by trial and error. Countless plays are recorded and remembered along with corresponding opponent tendencies. Coaches tend to find the optimum mix of plays subjectively based on a combination of experience, intuition, and tradition. Game theory, however, can provide the true optimum mix of strategies, assuming the strategy choices are clear and their outcome distributions are known.
On the football field, the equilibrium point is found by trial and error. Countless plays are recorded and remembered along with corresponding opponent tendencies. Coaches tend to find the optimum mix of plays subjectively based on a combination of experience, intuition, and tradition. Game theory, however, can provide the true optimum mix of strategies, assuming the strategy choices are clear and their outcome distributions are known.Recalling the example strategy matrix above, let's look at how a mix of running and passing would fare against a single defensive strategy. According to our example, if a defense always blitzed and the offense ran 100% of the time its expected utility would be +6 for every play. And if the offense passed 100% of the time its expected utility would be -5. We can plot those two points on a graph, and because we've defined utility as a linear function of preference, we can also draw a straight line between them (below). This line represents the expected utility of a given offensive strategy mix, from 100% run on the left to 100% pass on the right.
 If the blitz were the only strategy choice for the defense, then the offense's solution would be obvious. It should run 100% of the time, and it would expect a +6 payoff each play. But the defense has other options. The chart below adds the run defense and the pass defense as potential strategies.
If the blitz were the only strategy choice for the defense, then the offense's solution would be obvious. It should run 100% of the time, and it would expect a +6 payoff each play. But the defense has other options. The chart below adds the run defense and the pass defense as potential strategies.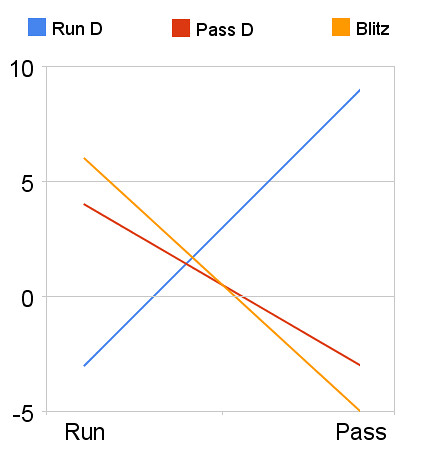 This chart of all possible strategies reveals the optimum strategy mix for both the offense and defense. Notice how the resulting plot forms a 'tee pee' shape between the y=0 line and the intersections of the defense strategy lines. This is where the offense's optimum strategy mix lies.
This chart of all possible strategies reveals the optimum strategy mix for both the offense and defense. Notice how the resulting plot forms a 'tee pee' shape between the y=0 line and the intersections of the defense strategy lines. This is where the offense's optimum strategy mix lies.Think of the chart from the defense's perspective. The defense can hold the offense down to at most y by choosing a certain strategy or strategy mix. From the offense's perspective, it can maximize its payoff by selecting a mix of strategies at x. The version of the chart below identifies the solution.
To recap, the x-axis is a proportion of running and passing by the offense, from 100% running on the left to 100% passing on the right. The y-axis is the payoff to the offense based on the strategy mix of the defense.
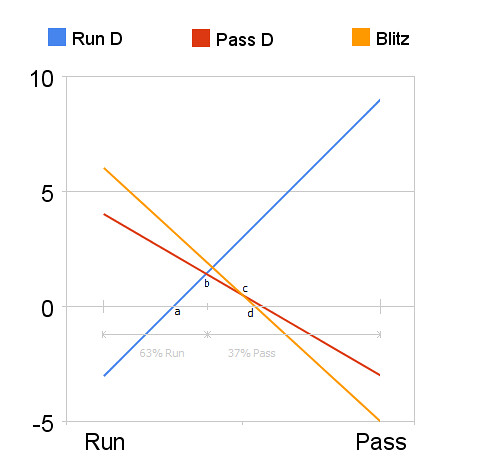 To have any positive outcome, the offense needs to select a pass/run proportion somewhere between point a and point d. To maximize its utility, it should select the proportion at point b. (Keep in mind that the left side of the chart represents 100% run, so the fact that point b is closer to the left than the right indicates the offense should run more often than pass.)
To have any positive outcome, the offense needs to select a pass/run proportion somewhere between point a and point d. To maximize its utility, it should select the proportion at point b. (Keep in mind that the left side of the chart represents 100% run, so the fact that point b is closer to the left than the right indicates the offense should run more often than pass.)Similarly, the defense should choose a mix of run defense (blue) and pass defense (red). The blitz strategy does not intersect at the offense's optimum (point b), so it plays no part in the defense's optimum solution assuming the offense optimizes. If the defense were to mix in some blitzes, the offense would be able to increase its expected utility to somewhere above point b. Only when the defense believes that a pass is more likely than at point c should it consider blitzing.
Further, we can use algebra to compute the equilibrium point. We know that the equilibrium lies at the intersection of the run defense and pass defense lines. They can be described as follows:
pass defense: yPASS D = 4 - 7x
At the equilibrium (point b), yRUN D= yPASS D. Therefore:
19x = 7
x = 7/19 = 0.37
Given the example, the offense should pass 37% of the time and run 63% of the time. Knowing this, we can also find the expected utility at the equilibrium point using either of the relevant defensive strategy lines. I'll use the run defense line:
y = -3 + 12(0.37)
y = 1.4
The point at which the defense should begin to blitz (point c) is where the pass defense line and the blitz defense line intersect.
blitz: yBLITZ = 6 -11x
yPASS = yBLITZ
4 - 7x = 6 -11x
4x = 2
x = 2/4 = 0.5
Only when the offense's probability of passing is >= 50% should the defense blitz. We can find points a and b similarly by setting y = 0 for the run defense and blitz equations.
Even though the example here is artificial, the principles of game theory apply throughout every football game. Of course, offenses aren't limited to two play choices. Their playbooks are famously complex. And defenses are not limited to three options. In fact, they're not limited to any number. In reality a defense has an infinite continuum of biases between run and pass, from goal line defense to prevent defense and everything in between.
These problems are really only a matter of scale. The algorithms of game theory can solve games with large numbers of strategy options. It can even handle strategy sets like a defense's, without discrete "pure" strategies. Plus, the problem lends itself to great simplification because much of every offense's playbook is composed of subtle variations of a few virtually universal NFL plays.
 Application of game theory hinges on true measures of utility. The real difficulty in applying game theory to football on a practical level would be to develop a valid measure of the preferences of the various payoffs in the game matrix. Yards or points would seem like suitable measures, but a 3-yard gain is far more useful on 3rd and 2 than on 3rd and 9. And a 3-point field goal is fairly useless down by 7 late in the 4th quarter. In a forthcoming article I'll attempt to solve this problem with a proposed utility function for football.
Application of game theory hinges on true measures of utility. The real difficulty in applying game theory to football on a practical level would be to develop a valid measure of the preferences of the various payoffs in the game matrix. Yards or points would seem like suitable measures, but a 3-yard gain is far more useful on 3rd and 2 than on 3rd and 9. And a 3-point field goal is fairly useless down by 7 late in the 4th quarter. In a forthcoming article I'll attempt to solve this problem with a proposed utility function for football.But next, I'll look at what effect a star running back might have on offensive strategy. Should it pass more often or less often? How will the passing game's effectiveness change. How should a defense react? We have intuitive answers, but we'll see what John Nash says.








"Further, if passing is far preferable to running, why should a team run at all? Hopefully that's obvious. An opposing defense could exclusively focus on defending the pass, dramatically limiting any expected gain."
This may be my favorite statistical topic, why do teams run the ball? In some cases running is empirically better: 4th and 1, 3rd and 1, 3rd and 2. In all other cases clubs consistently gain more yards and gain first downs at a higher rate when they pass instead of run. Since even Mike Martz runs the ball occassionally, commentators are left trying to justify the run because that's what clubs actually do.
I'm not sure a justification is needed. A common reason is the one I've quoted: teams run to "set up the pass", "keep the defense off-balance", "keep the defense honest", prevent the defense from "exclusively focusing on defending the pass", etc. Essentially this boils down to running the ball's suboptimal, but hopefully it will increase the expected gain from the passing game.
Teams often telegraph when they are going to pass. If Kurt Warner is flanked by 4 wide receivers and nobody is behind him, should the defense be surprised when they pass? I sure hope not. Defenses will switch to a nickel or dime package, and the offense will still throw the ball.
In 2007 teams passed nearly 89.7% of the time when faced with 4 or more yards to go on third down (regular season). Even if there wasn't a Warner/empty backfield combination telegraphing the play type any defensive coordinator should guess pass with that large a bias.
With such an obvious selection bias towards the pass game theory predicts that the 'surprise' run should net big yardage. It doesn't. Teams STILL gain more yards passing the ball and get first downs more often. Avg gain rushing, 3rd and 6 to 10 yards to go: 3.8 yards (5.9 yards for passing in same situation), First down %, 3rd and 6 to 10 yards to go, rushing: 18% (37% passing).
If teams selected plays on first and second down like they do on third down would passing still be better? I think so, but we may have to wait for Mike Leach to get an NFL job to find out.
ch-All very true.
Can I ask where you got your data?
This seems like an analysis of the original Tecmo Bowl. You got 4 plays to pick (2 run, 2 pass. Some teams have 3-31 ratios). On defense you better have good predictive skills or else you are toast.
Just as economists are fooled by the Nash Equilibrium, so can football tacticians also be.
Deception -- in football, misdirection -- changes everything. Act like you are convinced a running strategy will win (controlling the clock) and your opponent may take the bait. That is the time to pass. Act like you are going to pass, and then run (draw play). Or act like a run, then pass (play action).
Convince the defense that you have a plan and you know what they will do next. Script plays to catch them leaning, and when they lean, go the other way.
The soft underbelly of the market place is fraud. The same applies to football strategy. The most effective football play -- if both teams are relatively equal, which they generally are in the nfl -- is "nothing up my sleeve..."
There lots of potential deceptions that go beyond play selection: the trap, counter, reverse, HB pass, bubble screen, bootleg, etc. etc. etc.
But isn't it true that most defenses know not only of the possibility of deception but also virtually all the forms it can take/has taken? Don't DCs design schemes to minimize the possibility that any of these will work, or quickly adapt (over the course of the season) to the flavor of the month?
I think :) it's rare to see defenses or offenses "fooled" outright, in the way the OP describes (calling a run defense and failing to adjust to stop a pass, or vice versa). Most standard schemes (like the Phillips 3-4 or the 46) prescribe multiple roles to players out of base calls to account for precisely this problem; Belichick's scheme seems to work differently, but, let's face it, it's because the guy is the best in the business at knowing exactly what his D has to do to stop the other guys.
ON DECEPTION IN FOOTBALL
"I think :) it's rare to see defenses or offenses "fooled" outright, in the way the OP describes (calling a run defense and failing to adjust to stop a pass, or vice versa)..."
Deception (or more precisely, misdirection) isn't a one play proposition. The idea is to mislead enough to stay on the field (or to get the other team off the field). It's a matter of degrees, a matter of cumulative yards rather than big plays.
As anonymous mentioned above, what you want to do is catch the other team leaning, not completely bamboozled. The Pittsburgh DC is very good at messing up the chalk board -- players are not where they are supposed to be. But something as simple as a play action still needs to be set up. You need to "invest" in some poor yardage plays to show a tendency. When the defense starts to anticipate, you show the same play (run) but now it's based on what you've made the defense anticipate. You pass.
Misdirection versus brute strength. Those are the two factors in football you might measure.
"The best approach is to unpredictably sometimes run and sometimes pass, which game theory calls a mixed strategy."
Theory runs into reality sometimes and gets messy. Like Urban Meyer once said if you play a 2 high safety defense when I have 4 WR's and the LB's are split out to the apex between EMLOS & slot WR he won't call a pass play. Similarly if you leave a WR uncovered they'll bubble screen you to death...it is no secret. It is smart execution based upon what the defense relatively gives up.
In order to be useful to coaches this has to get eventually to specific runs (lead iso vs. over front) versus specific fronts and specific passes versus coverages(smash vs. cover 2). That takes a lot of film watching and statistical analysis but not the sort you are engaging in.
Please don't stop but someday try and do it from the coaches standpoint as well for fun. 2nd and 7 from your 35 yard line...what formation, what motion, what type or run or pass, and what counter will you run of this later? I think it will influence the future direction of your work. Good luck and please continue.
You have to also think about run/pass from the perspective of a player.
Suppose you're a linebacker in, say, a 4-3 defense. The ball is snapped, and the other team has just handed the ball off to a running back.
Stopping this running play will require, basically, every defensive player on the field to haul butt in either direct pursuit of the runner (for the defenders near him), or to make sure a cutback gap is defended (for defenders the runner may be running from).
You can't just stand there, even if the run is a sweep to the opposite side of the field. It'll take a team effort to make sure the ball carrier is contained.
This effort, in turn, will require hustle and intense physical contact on the part of most defenders. Defending the run, in short, is a pain in the butt.
Now let's say it's the next play. this time, it's a pass. You're playing a zone defense, and that's what you'll be doing most of the time. You drop into your zone, and maybe you run near a receiver who enters it, providing coverage. The ball is thrown downfield. It's caught - and you pursue, but you probably aren't going to be bumping into many people unless the ball carrier's right near by.
Or it's not caught. Or there's a sack. Either way, your work on the play is done.
If you play a pass-happy team, and you're a full-time starting linebacker who rarely leaves the game, you may drop back into your zone 40 times, but have to defend a pass or tackle a pass catcher only 5 or so times (depending on lots of factors, of course). That would be a striking difference if you were playing a run-happy team where you have to stick your nose into piles of blockers to contain a runner.
Why am I drawing all this obvious stuff out? Just to point out that a football play is more than just probabilities working themselves out. The difference in the physical experience between defending the run or the pass is another explanation for why teams bother to run at all.
You might like "The Art of Strategy" book.
The equation for run D utility should be -3+12x, not -3+9x.
So what's the answer for the defense here? How often should they be in run defense versus pass defense given offense's mix?
(yes, as noted above there is an error in the equations.)
Fixed. Thank you.
In this particular example, the defense would need to do the symmetrical opposite, guarding against the pass more often. Since the blitz is 'dominated,' the biggest vulnerability for the defense is playing run defense against a pass play. They should play pass D 63% and run D 37%.
In reality defenses don't have to play discrete choices, but can bias their scheme on a continuum based on how likely each play type is expected.
That is interesting - but I must be missing something if it is obvious that the defense should simply play the symmetric opposite.
If the parameters were changed (i.e. the slopes of those lines were changed) and the offense's optimal was 55% pass and 45% run would you still flip the numbers of for the defense? That doesn't sound right - you need to play the pass more if the offense becomes pass happy since like you said the potential to get burned playing run when the offense passes is so great.
(same guy as above)
Maybe I just don't understand how to view the graph from the defense's perspective.
Interesting article. I see that is optimal to run 63% and pass 37% in your graph. These numbers would be true if the right assumptions are met, and I am wondering how you could adjust theses numbers to the difference in score. For instance you are not going to run the ball 63% of the time when you are down by three touchdowns.
hmm how does this account for the Shovel pass that is run as a Power Run play??? hehe
Great article, yet I must disagree with simply constituting every pass play as the same.You can't categorize short passes as having the same probability for success or toss them in the mix as an average.As usual statistics need to be broken down to there finest detail if we want to find the truth.A series of 10 to 20 yard passes fall into a different category than passes thrown for on average 5 yard gains.So there is a third factor in determining play calling strategy and balance.