 Recently, I looked at onside kicks using an expected point analysis. We saw that "surprise" onside kicks could give a kicking team a big advantage. The break-even recovery rate would need to be 42% to make one worthwhile, and unexpected onside kicks are currently recovered 60% of the time.
Recently, I looked at onside kicks using an expected point analysis. We saw that "surprise" onside kicks could give a kicking team a big advantage. The break-even recovery rate would need to be 42% to make one worthwhile, and unexpected onside kicks are currently recovered 60% of the time.
But the expected point analysis only applies to "normal" football game situations. It does not account for the particular situations shaped by score and time remaining. For that we need to turn to win probability (WP).
Let's start with an example. It's the beginning of 4th quarter, and the kicking team has just tied up the game. An onside kick would clearly be unexpected in this situation, so we'll use the 60% recovery rate. A normally deep kick would result in a 0.44 WP. Getting the ball at its own 40 would give the kicking team a 0.56 WP, but a failed onside kick would result in a 0.40 WP.
WP(onside recovery) = 0.57
WP(onside failure) = 0.40
Given the 60% surprise recovery rate:
WP(onside) = 0.50
Further, if we approach the math another way, by setting the WP of the onside kick to equal that of a conventional kick, we can solve for the break-even recovery rate. In this case it would be 25%. A kicking team would need to successfully recover the onside kick only 25% of the time for it to be worthwhile. This rate isn't much higher than the 20% recovery rate for expected onside kicks.
The graph below plots the increase in WP for the onside kick attempt over a normal kickoff. Where the graph is positive, it is better to kick an onside kick, and where it’s negative, it’s better to kick deep.
The graph assumes the following: If the kicking team’s WP is currently 0.15 or below, the probability of onside success is 0.20. But if it’s above 0.15, the onside kick will be a surprise, and the probability of success is 0.60. (This is from what we learned in a previous post.) The x-axis is time left in the game, and the y-axis is the benefit in WP from kicking onside. I’ve selected 3 cases to illustrate, where the kicking team is ahead by 7, tied, and down by 7.
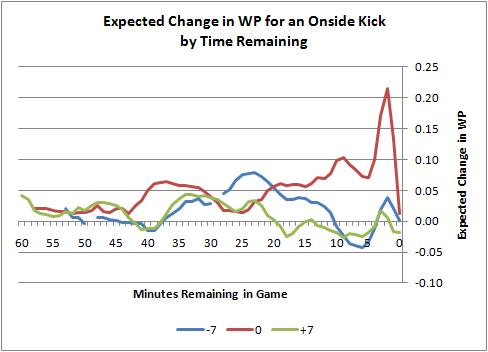
The lines are somewhat noisy, but they do show some very interesting trends. The feature that stands out the most is the large spike at the end of the game for when the score is tied. This is suggesting that a team that is kicking off with just 2-3 minutes remaining is much better off kicking a surprise onside kick. With that much time left, an opponent has plenty of time to score, and if it does, the kicking team would have almost no time to respond. Plus, a successful onside kick could be nearly fatal to the opponent, depending on the number of timeouts available.
Possession of the ball is absolutely critical in this situation. All things considered, the advantage of kicking onside increases the WP of the kicking team by 0.22 from about 0.33 for a standard kick.
As we found with the expected point analysis from the previous post, a surprise onside kick is almost always beneficial. It always depends on the game situation at hand, and time remaining is a critical component.








I understand the math, Brian, but imagine being the first coach to onside in a tie game with 2:30 on the clock....professional suicide. Although it certainly makes more sense for a big underdog where you have less to lose than, say, New England playing Buffalo or something like that. Interesting stuff....my brother's a high school coach and I've been sending him your articles - especially the one about that coach in Arkansas that never punts. Keep up the good work.
If a big underdog tied the game late, a good coach would be aware that an onsides kick, even from a normal kickoff alignment, is a real possibility. We've seen teams in recent years go for two at the end of a game when an extra point would tie the game, an onsides kick in your situation isn't that far off.
Drew, it would only be professional suicide 40% of the time. What would a coach like Jim Zorn have to lose?
Just eyeballing the chart, it appears that an onside kick, on average, increases a team's WP by about 3%. Maybe Brian could compute a more accurate number. So with about 5 kickoffs per game, a team that always onside kicks would increase its chances of winning by 15%. Over the course of the season, that would turn an 8-8 team into a 10-6 team.
Obviously a team that rarely kicked deep would lose the element of surprise and thus their success rate would decline. But as others have pointed out, your kickoff coverage when kicking deep would improve due to the uncertainty. So let's say that a team randomly kicks onside half the time at a 40% success rate. Even if the WP advantage shrunk to 2%, you'd still increase your chances of winning by 5%, which is nearly an additional win over the course of the season for an average team. I wonder how that would compare to the benefit of never punting.
You're right. Also, remember when you are talking about how the other team would adjust, remember that the biggest way to defend against a successful onside kick involves changing personnel. A kicker could always audiblize out of an onside kick if the other team had the wrong men on the field.
In the "what do you have to lose" department, I'm always shocked that losing coaches don't get a little more experimental. Think about the Wildcat. The Dolphins who (1-15 the previous year) were playing at the Patriots (18-1) the previous year. It was obvious what was going to happen if they played it straight. The Wildcat conceptually made sense but most coaches still wouldn't experiment with it. Yet if anything, I feel like teams like Buffalo and Cleveland are getting even more conservative. What the hell do you have to lose?
Math does not compute.
1) Kicking deep is 44% WP (opposition has 56% WP and gets ball at roughly their own 25-30 yd line)
2) Successful onside kick is 56% WP (You get ball at own 40).
Why would you have the EXACT same WP getting the ball at your own 40 as the opponent does getting the ball at his own 25-30?
It's really just rounding error, as those few yards don't make a big difference in the game's WP. The avg starting fld pos after a kick is actually the 33. The median is the 28.
But you're right in that it doesn't make the example very convincing. I'll adjust the example very slightly just for illustrative purposes.
After the Superbowl, it seems the Sean Payton must have read this article.
Where can I get the raw data?
Does this logic still hold after the kickoff rule change? I'd imagine the expected field position is around the 22 or 23 by now, although that ten yard difference is made up for by the 10 yards better field position if you recovered? Has anyone worked out the effect?
"Why would you have the EXACT same WP getting the ball at your own 40 as the opponent does getting the ball at his own 25-30? "
It's possible there could be some noise in the data. It's also possible that they could coincidentally be the same. By having the ball at the 40 you may score sooner. But scoring sooner would leave more time on the clock for the opponent to score. By having the ball at your 25, you may be more likely to run out the clock when you score so your opponent has no time left to respond.
Many time I have seen games where a losing team gets the ball with 2 or 3 minutes left in the game. They take the lead on a big play, but then the opponent has enough time to score and the team that scored quickly loses.
There have been a few times where teams let the other team get a TD so as to have time for their offense to score last.
Anyway, given time and field position are both factors, I can see how a balance effect could exist where maybe 25 and 45 yard line happen to have similar WPs.