 Back in 1997 I was spent Easter Sunday with a good friend. His brother, who lived in the La Jolla area of San Diego, hosted us for dinner. On the drive up the La Jolla ridge overlooking the Pacific, my friend pointed over to the right side of the road and said, "That's Junior Seau's house." I caught a glimpse of number 55, along with what looked like a dozen family members filing out of a couple vans in front of the house. They were the largest human beings I had ever seen. The women were large, the men were unimaginably large, and even the children seemed enormous. Junior somehow appeared to be the runt of the family. I got the impression Samoans were all giants.
Back in 1997 I was spent Easter Sunday with a good friend. His brother, who lived in the La Jolla area of San Diego, hosted us for dinner. On the drive up the La Jolla ridge overlooking the Pacific, my friend pointed over to the right side of the road and said, "That's Junior Seau's house." I caught a glimpse of number 55, along with what looked like a dozen family members filing out of a couple vans in front of the house. They were the largest human beings I had ever seen. The women were large, the men were unimaginably large, and even the children seemed enormous. Junior somehow appeared to be the runt of the family. I got the impression Samoans were all giants.
Last season there were 30 NFL players of Somoan descent, and 200 more playing Division IA college football. (Here's a list from 2008.) That's a lot of players from a group of people whose entire population could easily fit into an NFL stadium. Earlier this year 60 Minutes aired a profile on Samoan football, and if you missed it it's a great story. (I've embedded the clip at the end of this article. Edit--CBS has killed the link.)
Undoubtedly, the culture and character of the Samoan people are factors in their disproportionate level of success in football. But, as my drive through La Jolla suggested, hereditary traits may also play a role. Still, how can a single small island produce so many top players?
Like almost all human traits, the things that make a great football player great, like size, strength, speed or aggressiveness, conform to a normal distribution, also known as the bell curve. Normal distributions all share a certain shape in which there are lots of people near the average and steadily fewer people toward each extreme, known as the "tails" of the distribution.
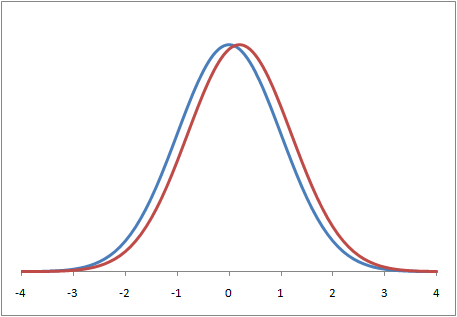
Suppose there are two different populations of people, and they had nearly identical distributions of a certain characteristic. Their only difference was that each population's average differs by a relatively small amount. If one population is, on average, only slightly larger, stronger, or faster than the other, there will be nearly the same number of people from each population around their average values. The graph below plots the distributions of such a scenario. The x-axis represents the level of any characteristic of interest, and the y-axis represents the proportion of a population that possesses that characteristic at that level.
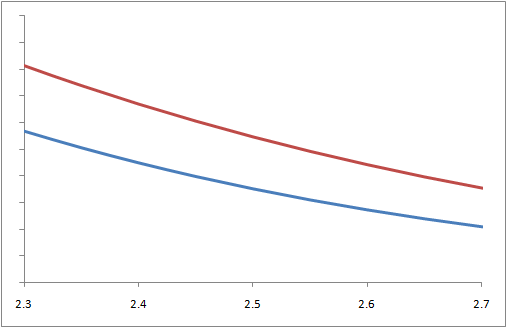
You'd think that there would be a correspondingly slight difference among each population's elite, but that's not the case. A slight difference in the average value of a characteristic means there will be extreme differences in the tails. Notice that as we zoom in on the right tails of the distributions, the further out the tail we go, the more drastic the difference:
For example, men and women have different average heights. In the US, the average man is about 8% taller than the average woman. But at 5'10" there are 30 men for every woman, and at 6'0" there are 2,000 men for every woman. In other words, a just 1.08 : 1 ratio of averages translates into a 2000 : 1 ratio of men to woman at 6-feet. The point is, a relatively small difference in the average value of a characteristic can result in drastic differences in the proportions of populations toward the tails.
If, on average, Samoans are only slightly stronger, faster, or anything else considered good for football than the rest of us are, we'll see vastly disproportionate outcomes in the right tails. And the right tails are where NFL players come from.
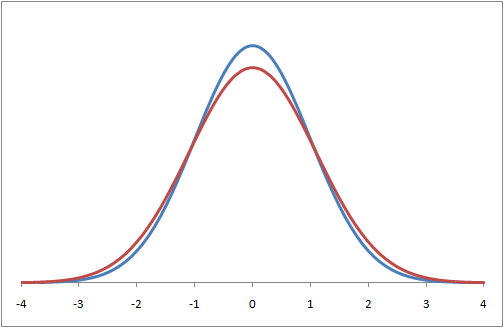
Further, even if two populations share the same average value of some characteristic, a difference in variance would cause the large disproportions in the tails. In other words, the more "spread out" a distribution is, the fatter the tail will be and the more likely there will be outliers.
As we zoom in on the right tails again, we see a disparity in the number of outliers within the respective populations.
When there is a combination of both effects, a difference in averages and a difference in variances, the effects are multiplied and the resulting disparities can become extreme. I suspect that's part of the story of Football Island, and there's a broader lesson here too.
Samoans probably aren't much different than the rest of us, and in fact, no particular group of people are really that different from another group. There may truly be slight differences among groups, but they are probably quite small. When we focus on the extremes of the distributions, either in the right tail, where we get our superstars in athletics or any other field, or in the left tail, where we see the less successful elements of society, we're likely to form misleading impressions. Not to sound too preachy, but perhaps some part of our prejudices are largely the result of a mathematical property of nature.









A wise and novel application of statistics. Excellent.
I never took Burke for a believer in eugenics. Shameful.
Larry Summers said pretty much the same thing and got into a heap of trouble for it.
Jimmy the Greek also was ostracized for making the same observation - although he obviously didn't articulate himself as intelligently as does Brian. Even worse, he made his comments in regard to black Americans, which is a more racially-sensitive subject (in this country) than is the subject of Samoans. Unfortunately, the mass of poorly-educated and PC-sensitive people in this country have no ability to distinguish between racism and the simple observation that some populations of people may have "fatter right tails" when tracking a particular characteristic.
This is NOT a Jimmy the Greek observation. My point is the opposite. Our differences are tiny, not large, and it's only due to a peculiar property of the normal distribution that our differences *appear* magnified. This misleads us into thinking our differences are larger than they are.
I'm a believer in genetics, not eugenics. I'm hoping whoever wrote that comment above doesn't really understand what eugenics is, because it's a terrible thing to accuse someone of.
What's shameful is some some anonymous idiot trolling a website making irresponsible remarks on an article he clearly didn't take the time to read, since there is nothing shameful about what Brian wrote.
Well-written, Brian. Unfortunate that to even suggest there are differences between people (no matter how small) will result in controversy in this environment. Geez!
OK, I should probably just shut up about this, but...
I understand that your post is not, directly, a "Jimmy the Greek observation". Making any reference to slavery is politically taboo and you certainly did no such thing. But I am convinced that he would have been run out of CBS even if he had said something as benign as, "Blacks, as a whole, may have some small advantage due to genetics." Because to suggest that any race of people has any possible advantage, even in the slightest way, is a no-no in our society. We're supposed to completely ignore the over-representation of certain races in sport or, at most, we're supposed to attribute it to economics.
As you've shown with your generic analysis of binomial distributions above, an over-representation of a given race (like Samoans) MIGHT be a sign of a very slight genetic advantage. It also MIGHT be that they simply experience a greater variance in the key factors that denote NFL success. Or it MIGHT be something completely unrelated to these factors (or, more likely, a combination of many factors).
The point is that racial tendencies (genetics) CAN play a factor in such things. It's not racist to point this out.
I getcha'.
One thing I'd point out is that the principle in the main post holds for any normally distributed characteristic, not just genetic characteristics.
This really shouldn't be controversial at all. If you believe families have certain genetic traits, then you can think of the 65,000 American Samoans as simply a large family.
Wikipedia says the average male height in Mongolia is 5'6". In the Philippenes it's 5'4". In the US it's 5'10". Body mass for each group is very different too. Are those differences genetic or due to nutrition or something else? I don't know. I just know the averages are different. I guess that makes Wikipedia an evil eugenicist.
I've been thinking about this recently too. I looked at two athletes who were 6'1", 215 lbs and 6'7", 230. Although they could be an NFL wide receiver (Andre Johnson) and an NBA small forward (Carmelo Anthony) at that size, they're both MLB pitchers. They're also both white.
Obviously the skill sets are different, but I bet all four of them could have been successful at other sports had they practiced them. Along the same lines, Tracy McGrady likes baseball more than basketball and was a top baseball recruit (he even said he's considering becoming an MLB pitcher sometime in his mid-30s), but yet he chose to play basketball. Why? I think it's cultural.
I can certainly understand the distribution to be shifted to the right - ie a big family as you mentioned in the comments. But what would make the standard deviation be larger? I don't really understand how that would work in a population. If you could somehow control for larger standard deviations that could be helpful in a lot of cases.
This comment has been removed by the author.
A friend of mine is studying liver cell sizes from an evolutionary biology standpoint. Given an ideal size, a species can achieve that size through a medium number of medium sized cells, a large number of small cells, or a small number of large cells.
All three achieve the same optimal liver size, but the medium cell size has the lowest standard deviation. This is likely to be more stable, but the larger standard deviations make the others more capable of surviving an environmental change by increasing their tail ends.
Just an example.
But what would make the standard deviation be larger?
From a purely statistical standpoint, it is because they are a subpopulation. Consider two subpopulations identified by something with no bearing on athletics: red heads and people with wisdom teeth removed. Will those two group have the same SD as the general population? Almost undoubtedly no, they won't. That's just the way subpopulations work.
If we get a larger SD for red heads and smaller for the wisdom teeth crowd, we'll see more redhead pro athletes, even though red hair doesn't have any impact on athletic achievement.
There may be no genetic reason* for a difference in SD among Samoans. Remember, genetics is the random attempts to be good enough, not optimal.
*but I wouldn't bet on it.
It's striking how much anger this post, which clearly understates the sizable genetic differences in size and muscle mass between Samoans and most other racial groups, has generated. Before the first Samoan became prominent in college football (quarterback Jack Thompson, "The Throwin' Samoan"), the great writer Tom Wolfe pointed out in his 1970 book Radical Chic & Mau-Mauing the Flak Catcher:
"Have you ever by any chance seen professional football players in person, like on the street? The thing you notice is not just that they're big but that they are so big, it's weird… From the ears down, the big yoyos are just one solid welded hulk, the size of an oil burner… Well, that will give you some idea of the Samoans, because they're bigger. The average Samoan makes Bubba Smith of the Colts look like a shrimp. They start out at about 300 pounds and from there they just get wider."
Deer Brain:
As a male I'm offended you would point out that I am a moron and for what its worth my deviations (standard or otherwise) are my business and done in the privacy of my cell.
Thank you Brain.
That's a great quote, but the scene from Pulp Fiction about the Samoan who gave Marcellus Wallace's wife a foot massage takes the cake. It's un-quotable here in polite company, but you can Google it.
To be clear, however, I guess it never dawned on me that the Samoans are "a race." There are only about 65,000 of them. I would consider them a unique "island population," which is a sub-group of some other race, Pacific Islanders I suppose.
I saw Pulp Fiction in Pensacola Florida.
There was a lot of non-standard deviating in that movie when they brought out the Gimp.
Is that offensive?
I think the Gimp was dysgenic!
Thank you very much. I'm here all week.
Regarding the male/female IQ thing. Males are overrepresented at both extremes in all species where males compete for females. The reason is because as with any polygynous species a few % of males have sexual access to the majority of females (although forced monogamy serves to counter this, hence why contrary to popular belief monogamy is beneficial for the majority of males not females). To be a male and have a high chance of reproducing successfully you have to be at the upper extreme. this is not the same for females, as all females reproduce at pretty much the same rate regardless of physical attractiveness, intelligence, etc. Therefore the best evolutionary strategy for producing male children is to gamble. Either win big and pass your genes along or lose big and don't (the middle road is also considered losing). Note that forced monogamy has created a society where average men are able to pass their genes along, however evolution has not yet caught up (and probably never will).
I absolutely love reading the articles/posts on this site. They are intelligently written & well thought out & I'm feeling smarter already haha
AWESOME!