 NFL offenses generally run too often on 1st down. Accounting for the relative gains of each play type, and accounting for the risks of turnovers, offenses should pass more. There is currently an imbalance, where teams are too often running directly into defenses that are expecting runs.
NFL offenses generally run too often on 1st down. Accounting for the relative gains of each play type, and accounting for the risks of turnovers, offenses should pass more. There is currently an imbalance, where teams are too often running directly into defenses that are expecting runs.
Game theory tells us that when there are two strategy options, like run and pass, the expected payoffs for both options should be equal. You really don't need game theory to intuitively understand this. If one option yields a better payoff, then it should be chosen until the opponent responds with a strategy change of his own. Eventually, as the opponent responds, the payoffs for the two options equalize. The point at which the strategy mix equalizes payoffs is known as the minimax, or sometimes called the Nash equilibrium. The resulting strategy mix, or run-pass balance in this case, produces the best overall, long-run payoff.
When there are two strategy options and one of them yields a much higher payoff, it tells us two things. In this case, passing is more lucrative than running on 1st down, and this tells us: 1) offenses should be passing more often, and 2) for now, defenses should continue to be more biased toward stopping the run.
Recent Studies
There have been two recent studies that looked at the same issue, but both of them suffer from the same flaw. Freakonomics author Steve Levitt teamed with Kenneth Kovash to publish 'Professionals Do Not Play Minimax.' Another paper called 'Risk and NFL Playcalling' was recently presented. Both papers fail to account for the context of the game by considering time remaining and score difference. For example, a team ahead will use the run to work time off the clock, sacrificing optimum scoring but increasing its chances of winning. The time-value of the run is not captured.
A Solution: 'Normal' Football
One simple, but partial, solution I recommended was to limit the data to what I call 'normal' football situations. Normal football is when score and time are not significant considerations. The score is close, so teams are playing with a conventional and balanced risk-reward mindset. And time is far from running out in either half, so neither team is adjusting its play-calling because of the clock. So I took my own advice and ran my own numbers. I looked at plays where the score was within 10 points and the game is either in the 1st or 3rd quarter. Ultimately, the goal is to look at situations where neither team is desperate or hurried, and both teams are still playing a game of maximizing their net point advantage.
I'll also improve on previous efforts by examining play values of runs and passes according to field position. We'll see that the relative value of the runs and passes change near the end zones.
Expected Points
To value plays, I used Expected Points (EP). Every down and distance has a potential point value at each yard-line on the field. The values are determined by averaging the point advantage offenses have historically gained given a particular combination of down, distance, and field position. The key to understanding EP is that it not only accounts for points scored on the current drive, but it accounts for points eventually scored by either team on subsequent drives. For example, a 1st and 10 at midfield is typically worth 2.0 EP. A 2nd and 5 at an opponent's 45 is worth 2.2 EP. So a 5-yard gain on 1st down at midfield would produce +0.2 EP. This method factors in risks such as sacks, fumbles, interceptions, incompletions, penalties, safeties and everything else. If the question is, 'Does it factor in _____?' the answer is yes.
Results
If we look at all runs and passes on 1st down and 10 (or goal), and average the EP gain for each type of play, we can measure the payoffs. The graph below plots the EP gain for 1st down runs and passes according to field position. For example, at an opponent's 31-40 yard lines, the average pass results in a gain of 0.10 EP, and the average run results in a gain of 0.01 EP.
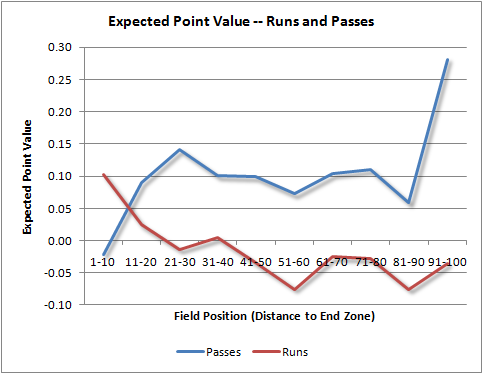
For the vast majority of the field, the pass has a higher average payoff. Runs have a higher payoff only inside final 10 yards before the end zone, so it appears teams are passing too often there. The discrepancy is especially apparent when an offense is backed up near its own goal line. This difference even accounts for the likelihood of a sack, or interception in such a vulnerable position. There are relatively few pass attempts in that situation, but still enough for a reliable estimate (402 of them).
In fact, for most of the field, the average value of a run is essentially zero or negative. This makes sense because a 1st down play needs at least 4 yards to be at least break-even in term of value, and most runs go for 3 yards or less. Between the 20-yard lines, 55% of runs on 1st and 10 gain less than 4 yards. The majority of runs on 1st down are actually setbacks.
Here is how the league-wide run-pass looks in recent years. The next graph plots the percentage of run plays on 1st down and 10 (or goal). Teams increase their tendency to run near both end zones.
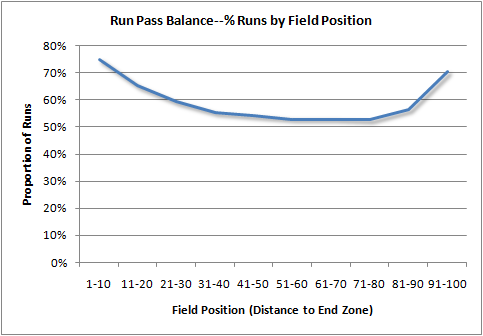
Right now, we can't say what the optimum 1st down run-pass ratio should be. But we can say with high confidence that offenses would be better off passing more often. Because 1st down is widely known as a running down, play-action fakes are very effective, and I would guess that's primarily where the pass gets its advantage. As teams pass more often on 1st down, the effectiveness of play-action will suffer. But meanwhile, as defenses are forced to defend more against the pass, runs will become more successful.
We can repeat this same analysis for other down and distance combinations. For example, are teams running or passing too often on 2nd and long? What about 3rd and short, etc.? I'll be rolling out articles in the near future with a similar analysis for other situations.
The usual caveats apply.This is a baseline for the league as a whole, but the EP curves could be tailored to individual teams and opponents. Play calling is never as simple as just run or pass, and there are many different types of passes, ranging from deep bombs to short screens. Additionally, there is some amount of bias in the data. Teams that are good in passing would be expected to pass more often, and teams good in running would be expected to run more often. In other words, we can't just tell the 2009 Browns to pass far more often on first down because their particular expected payoff for passing may not be any better than for running. Still, the league-wide difference between running and passing is so stark that we can still make a general conclusion.
End Notes: Data consist of runs and passes from all non-preseason NFL games 2000-2008, limited to the 1st and 3rd quarters when the score is within 10 points. There are 21,537 passes and 28,036 runs in the study.
Offenses Run Too Often On 1st Down
By
Brian Burke
published on 11/23/2009
in
coaching,
game theory,
run-pass balance,
strategy
Subscribe to:
Post Comments (Atom)








You analysis does not take into account the need to run in order to set up the play-action pass. A play-action pass relies on the fact that defenses need to account for the run.
Therefore, I would expect the optimal run-pass ratio to be slightly in favour of the run vs. the numbers your approach would produce.
One way to account for this would be to introduce play-action as a third stategy option (if this is possible with your data).
Joe. That's exactly the point. Teams are running more often than they need to in order to 'set up the pass'. Teams should not be sacrificing a negative play 60% of the time in hopes that the other 40% is more effective.
um - yes you're right.
Not really sure where my brain was going with that one!
Hi Brian - I know you said that everything is accounted for, but I've been meaning to ask if you include time-outs remaining in your analyses. It wouldn't make sense to here, but I don't remember it coming up in your Pats-Colts discussions.
This is very interesting, but you're missing something really major - decisions are optimal at the margin not at the average. This is a point most economists know, but is not widely known or applied by other disciplines. Basically, if a team is rushing/passing at a 1:1 ratio, they should consider the value of one additional pass attempt, not the average value of all the pass attempts that made their ratio 1:1.
Thus, we expect the MARGINAL value of a rush to equal the MARGINAL value of a pass attempt. And there is no particular reason that we should expect the average rush to equal the average pass attempt.
It helps to consider an extreme case - where a team rushes on EVERY play. This is almost definitely not optimal, because then the defense knows you are going to run and put 9-10 players in the box, and thus the marginal value of a pass is enormous (throw a bomb, get a ton of yards). However, as you decrease the amount of runs and increase the number of pass attempts, the marginal value of passing goes down and the marginal value of rushing increases. It is easy to see that the optimal is where these values are equal. However, in our example, it is also clear that the average pass is inflated by the huge value of that very first pass which will go for 50+ yards almost every time.
Statistically, it's a much harder exercise to try to calculate that marginal value of rushing or passing, but it is definitely the theoretically correct approach.
Out of curiosity, could there be a complication where games are more likely to be within 10 points in games where teams run a non-optimal strategy?
For example, say the Saints pass/rush at the minimax point. Would that not make it more likely they have leads greater than 10 points and therefore are not included in your study?
Overall, I still think your conclusion is correct.
How is it that both runs and passes have positive value within the 20? I would have thought the combined EP of all plays was zero, but obviously not. Can you clarify that?
Guy-That may be true, but this is a subset of all plays--just 1st downs.
Andy-Thanks for the great comment. I know we've been around on this topic before, and I've read up a little. But still, forgive my ignorance--I'm not an economist. But here is what I understand:
For a consumer buying a basket of goods, it's true that the last dollar spent will equalize marginal utility across all possible purchases. This is for a decision-maker in an open, free market of goods who is looking to maximize satisfaction.
However, the run-pass question in football is a 2-player zero-sum game. And that's where the distinction lies. Whatever gain I make, my opponent loses an equal amount. If I have 2 options, I should chose the strategy mix that maximizes long-run utility, which here means maximizing net points. Coaches are not purchasing a basket of goods in a market. They have 1 of 2 choices (in my simplified model), each with equal cost (1 down).
Another thought I had is that what you describe is descriptive, i.e. what coaches tend to do, and what I describe is prescriptive, i.e. what coaches should do.
Am I making any sense?
Brian: I don't see why the down would matter. The EP at 1st down already incorporates what will happen on the next play (on average). So the EP after that next play should be the same (on average), yielding a change of zero. The EP for passes and runs should add to zero (except for downs/yards where a significant number of kicks are made).
Andy, Brian:
The question of whether to maximize long-term utility or marginal benefit should collapse to the same solution in this case, essentially based on the zero-sum argument Brian makes. This is a good thing, otherwise it would be quite a pain to try to analyze coaching decisions. In fact, I think this is one of the reasons that sports are such a tempting setting for the analysis of decisions in markets.
Guy, I think you're right. Perhaps my baseline EPs are a little off. Near the end zones is where the data is the thinnest.
Intuitively, I see what Guy is saying. Descriptively, coaches tend to run more often than they sould pass. However, there seems to be a lot of situations in which running is both the inferior decision, and also a positive decision, at the same time.
At ~12 yards from the end zone, the lines cross at 0.05 points. If the teams already know that, then how come that 0.05 EP isn't already applied to the total EP value before the snap?
It's like probability. If your WP is 0.50 at a given point, a bad decision should not then lead to a 0.51 WP. By definition, the good decision WP would be higher than 0.51, and that probability tree would make no sense.
Shouldn't an inferior decision lead to a decrease in EP for the offense, and an increase in EP for the defense?
Ignore me ^^ I posted that before I realized you responded to Guy. :)
Could it be a rounding error? I noticed that these EP values are rounded to the nearest .01, which is more precise than the EP values that I saw in the fourth down study.
It looks like across the board the expected EP for a first down play is in the range of .03 to .05. As Guy and Jonathan have pointed out, this doesn't make any sense unless there's some crazy third type of play teams can run which really sucks. I'm thinking the baseline EP may be a bit off across the board.
Brian - this site is outstanding and the way you have built it up have carried yourself throughout is exemplary. I have one concern about this article, which is that I would wager that good offenses tend to pass more, so your numbers are biased because the passing EP numbers are overweighted with good offenses (I could be wrong). I checked the ratio of pass attempts to run attempts + pass attempts for the top ten scoring offenses of 2009 and it is 56.6% vs. 54.5% for the bottom ten scoring offenses, so there may be some validity there. I would expect the top scoring offenses to be winnning more games and thus running the ball more in the 4th quarter, so the effect in the 1st/3rd quarter data could be even more pronounced. I don't know if the dataset is large enough for this but I would be very interested to see if your results hold up if you would the results for good offenses vs. bad offenses.
This is a good generalized study. And I like the use of EP for analysis. However, I would think that the next dimension for this would be comparing the percentages for certain teams given different players abilities. I can't imagine that it isn't a good idea for the Minnesota Vikings to run on 1st down. Maybe so? Also it could also be that defenses usually play the pass on first downs and the subset of more succesful passing plays that you are seeing is a reaction to bad Defensive play calling or blown coverages. However, it is a good general article that will spark more interesting questions to be answered.
I believe the across the board positive EP is explained by a type of "play" that wouldn't be accounted for - that is a penalty. If the team with the ball commits a penalty on first down, their EP surely goes down but it doesn't count as a play official and so wouldn'tbe picked up by the model.
I think I know what the problem may be. On each play I have a starting EP and ending EP. EP Added is just EP2 - EP1. I'm not sure if my EP2s are correct for plays on which there is a score, which might explain the upward bias near the goal line. I'll check tonight.
Nope. Scoring plays look good. Now I think I may have overvalued TD scores. I have 6.40 EP for every TD, but the true value might be closer to 6.30 EP (7 points minus 0.70 for the value of the kickoff) or even less. That might be the difference.
Brian: Any chance that on plays which produce a TD your EP2 does not account for the expected points of the opponent on next possession? If so, but the EP1 did factor that in, that might explain the curves. (I'm assuming that runs account for a larger share of TDs the closer you get to the endzone.) It would also exaggerate the spread between runs and passes, I'd think.
Also, you mention here that a 5-yard gain on 1st down is worth about .2 points. Yet in your EP article, you suggest the value is zero: "Suppose at any given yard line, a pass falls incomplete on 1st and 10. Second down and 10 represents a drop off of about 0.5 points expected. Second and 9 represents a slightly smaller drop off, until at about 2nd and 5 when the expected points are approximately equal to those for 1st and 10." I assume the .2 is correct. Have you changed the methodology since that article was posted?
Yes, the original EP article was really just a first stab at the topic. I had a shiny new database and was only estimating 2nd down values.
1st down and 10 EP values are easy because there is so much more data. 2nd down data is spread among many to-go distances, and they need a good deal more smoothing.
Brian,
Economics is about marginal analysis in a lot of places, not just in a free open market economy. A first principle of optimality is that margins must be equal. This does not depend on the existence of a market or not. If we're considering two goods (like passing/running, or apples/oranges), marginal analysis is correct if 1) the person wants to maximize something and 2) they choose some of both goods, ie both run and pass. If these conditions are met, then the marginal benefit of both actions will be equal. I can show show this technically if you want, it falls out immediately of a maximization problem.
This is true in 2 player zero-sum games as well as a open-market economy. In 2 player zero-sum games this is exactly the case when pursuing a mixed strategy is optimal. The player is indifferent between options A and B, ie the marginal gain is the same, and so they are willing to mix over the possible options. Otherwise they'd choose option A everytime.
I'm trying to think up a clean example of how averages are misleading in analyzing run vs pass. I'll see if I can't put together a little numerical example or something. I also don't understand how the zero-sum nature could change the average vs. marginal analysis. I will think more about this, but if someone could elaborate that would be great.
One final thought I had is that, even if the average equals the marginal as is assumed here, why is the conclusion that teams should pass more? Isn't another possibility that defenses should defend the run less and the pass more on first down?
Andy,
I think Brian is presenting the marginal gain per run or pass play based on the prevailing NFL strategies. The one thing we can't look at is what the marginal gain per play would be if the prevailing strategy was a different mix. So Brian's model would break down if the marginal return per pass changed significantly from a 45% first down mix to a 50% first down mix.
Brian: Thanks. I think you're right to look at scoring plays as possible source of problem, since runs are much more likely to result in a TD at the very yardages where the run EP rises relative to the pass.
An unrelated question: do you have a post where you explain how you make the adjustment for opponents' next possession (.7 points)? Ideally, it seems to me EP at any given moment should reflect the net point advantage a team with the ball has over the remainder of the half. Is that right?
Brian,
Have you done any analysis on the play-action pass? One comment made by the announcers during yesterday's Colts v Ravens game was interesting. They noticed how the play-action pass impacted the defense in spite of the fact that the Colts running game is not that great and their passing game is such a threat.
Is there any evidence that the old adage of 'establishing the run' is true, or do play-action passes work just as well on teams that can't/don't run?
How do pre-snap penalties get calculated in? You usually can't tell whether a 5-yard false start or delay-of-game penalty was going to turn into a run or a pass. Could this be a partial cause of the expected point value for 1st-down plays not summing to zero? It seems that even getting a snap off is a +EV accomplishment for the offense.
- Person
If I remember correctly, the EP by field position graph was pretty linear, crossing 0.0 at your own 15 yard line. So to evaluate runs and passes by EP just seems to be saying pass plays on average gain more yards than runs. Which of course is true.
The conventional argument is that run and pass plays work together, so that the 3-yard run on 1st down leads to the 7-yard pass on 2nd, etc. Looking at the first play in isolation would lead to an error, since the second play wouldn't have been there without running the first. Certainly the hypothetical team that passes every time(which is what your analysis suggests for 1st down, but I'm guessing the graphs look the same for 2nd and 3rd) probably wouldn't be successful in real life.
So what we might really care about is probability of getting first down after running on 1st and 10 versus probability of first down after passing on 1st and 10. I'm curious what the historical data would say to that and if it sports the convetional wisdom.
Brian,
To take an (imperfect) analogy from poker: against a tough opponent, sometimes we have to make a -EV call on the river (instead of a 0 EV fold) in order to (get him to keep betting good hands so we can get paid with our better hands)/(prevent him from bluffing at will with his trash hands).
You may well be right that offenses run too much on first down, but I'd still expect EP(pass) > EP(run) at the optimal run-pass mix. It'd be a disaster if at the strategy where EP(pass) = EP(run) both values turned out to be 0.01.
Regarding marginal analysis, a simple example may illustrate.
Say a business produces two products, gadgets and gizmos. It wishes to invest its resources to produce them in the most profitably optimum mix.
Producing more of either will increase sale revenue but reduce the price of the item sold (increased supply = lower price).
The optimum is to reach the point where the profit of selling one more gadget = that of selling one more gizmo. (Until that point is reached, obviously, it is most profitable to sell another of the most profitable item.) This objective is equal profitability at the margin, from the sale of one more gadget/gizmo.
Now say that initially for whatever reason sales of gadgets are much more profitable than those of gizmos. Thus you will incease sale of gadgets until the revenue from the marginal sale of another gadget declines to equal that of another gizmo. Objective achieved!
However, if you then look at the *average* profit from sales of the two items you will come to a different conclusion. On average, sales of gadgets are still much more profitable than sales of gizmos.
If you think the objective is to equalize average profitability from the sales of the two items, you will say "produce more gadgets! more gadgets!" and invest in doing so. And you can acheive that goal -- by driving the marginal return from additional gadget sales so low that you are maybe taking very bad losses on them.
The result here is that the profit maximizing strategy is investing to produce gadget sales that have a much higher average profit than gizmo sales.
If marginal profit from the two items is equal, the higher average profit is not a sign of any missed opportunity from selling too little of the "most profitable" item -- trying to equalize the average profitability would be the mistake.
The analogy here is that the team is investing to get the biggest profit by producing passing plays and running plays, with passing being gadgets and running being gizmos.
It's 3:40 am as I write this so I am not going to pursue whether the analogy is correct or not -- I can think of arguments both ways, but my addled mind at this hour is too tired to try to judge their merits.
However, *conceptually*, it is true that playcalling should seek to equalize *marginal* return from passsing and running .... and that this being so, much higher *average* returns to passing are not automatically inconsistent with a correct play calling mix producing equal returns at the margin.
The issue from there would seem to be whether or not in football average returns = marginal returns or not (the firm/team is a "price taker" regardless of its production choices rather than a "price setter" via its production choices).
If anyone cares, I'll think about that another day.
I think this whole discussion about marginal and average utility is off. In football, there should be no difference between marginal and average utility. After each play, the coach makes a decision which one play to run next. He should chose the play with the highest marginal utility (run if one more run will net more EP, pass if one more pass will net more EP). If his expectations of the marginal EP are not biased, these marginal utilities will aggregate to average utilities over time. Ergo marginal utility equals average utility.
To put it another way, given stable percentages of passes and runs, increasing the percentage of runs in equilibrium does not just lower the marginal value of runs but the *average* value of runs.
The point about it being a two person zero sum game is also correct as in that type of game both strategies (here run and pass) should net the same average outcome given the opponents optimal mix of strategies.
I wonder how penalties would affect the results for instance if passing plays result in negativd penalty yardage frequently then you could get bias.
Simon,
The problem is that the other coach also knows what option has the higher EP, thus forcing us to go with the other option sometimes.
The key difference between runs and passes, aside from the lower average gain for passes, is the greater certainty of progress from a run. With a pass you'll face 2nd-10 about half the time, but that will happen much less often on a run play. There are two consequences of this that may explain some or all of Brian's finding of an apparent inefficiency.
First, EP for passes incorporates some of the value of subsequent runs. Let's say a 8-yard completion on 1st down is worth .5 EP (all numbers for illustration only). Maybe .25 of that is field position, and .25 is the very high probability of 1st down conversion. But why is the conversion so likely? Because 2 runs will invariably get you a first down (maybe 90%?). In contrast, two consecutive passes at that point might yield a conversion only 70% of the time. So teams will run a lot at 2nd or 3rd and short yardage, and usually convert. BUT, that's already incorporated in the EP2 on your pass play. The 8-yard pass stole value from the future -- kind of like cash for clunkers -- and the subsequent run plays are awarded very little EP because those 2 yards were already taken for granted by EP. But the near-certainty of some progress offered by the run has tremendous value in many circumstances.
Second, a lot of this disparity will depend on the exact valuation of an incomplete pass vs. a short yardage run gain. Let's say Brian estimates an incomplete is worth -.5 and a 3-yd run is -.2. If the real numbers are -.6 and -.1, the apparent advantage of passing probably disappears. As Brian acknowledges above, the 2nd down (and I assume 3rd down) EPs are much harder to calculate. I'm NOT saying his calculations are wrong -- I have no idea. Just saying that this analysis will be highly sensitive to even small adjustments in the valuation of 2nd and 3rd down yardages. The down/to-go factor will often outweigh field position in importance (EP at opponents' 35 and 4th-and-long is probably less than 2nd-and-1 from your own 35).
I did some digging and it looks like the net positive EP comes from plays classified as neither runs nor passes. Most common are what are called 'aborted' plays in which there was a fumbled snap or a QB trip. It is unknown whether these were intended as runs or passes, and for whatever reasons they tend to occur near the goal line.
Guy-But if runs tend to be counterproductive, then certainty is bad. Wouldn't the EP concept account for 'certainty of progress?' In other words, according to this result certainty is overrated. Certainty might help the OC keep his job by playing to convention, but teems appear to be sacrificing net point advantage for the sake of it.
"But if runs tend to be counterproductive, then certainty is bad."
Certainty can have value because of the need to convert within 3 downs (OK, 4 if the NFL listened to you, but let's say 3 for now). Raising and lowering the probability of conversion seems to me the heart of scoring (similar to the ball-strike count in baseball).
This season teams are gaining 6.2 yards per pass attempt, and 4.3 yards per run attempt. I don't know the SD of run yardage, but let's say it's 2.5 yards. Now suppose the run SD became zero -- every run gained 4.3 yards (but teams continued to pass and run at the same rates as now). My guess is that the average EP for run plays would be about the same -- that a gain of 4.3 yards is worth about 0 EP on average. Is that correct? If so, your analysis would still say teams should pass more than they do. But that would of course be 100% wrong. The correct strategy would be to run 100% of the time, convert every time, and score a TD every possession.
Or consider a sequence of one 6-yard pass and two 3-yd passes for a 1st down and total gain of 12. I believe the total EP for the two runs will be negative, while the 6-yard pass will be strongly positive. Does that allocation seem correct to you? The runs (combined) and the pass contributed equal yards; all were essential to achieve the conversion.
The pass has high value because it yields a very high conversion probability. But isn't that in turn a function of the runs that invariably follow? Yes the pass gets more than 100% of the credit.
Also, could you share what the EP curve looks like by yards-to-go at 2nd down? Is it linear, or is the difference between 7 and 4 yard gains, say, larger than the difference between 1 and 4? That might help clarify my thinking about this.
The 6-yard pass and 3-yd (runs?) may have contributed equal yards, but did not contribute equally: the runs took two plays to manage what the pass did in one. I would expect the pass to have more EP than a run for sure and possibly than both runs combined.
This would also make sense given the 3-down universe in which most coaches confine themselves. Gaining 3 yards can be helpful but will obviously not give you success in bulk because you'll be punting on fourth-and-one (in this universe). Gaining 6 yards is extremely helpful in bulk because third and fourth downs would never occur.
Andy, Jim,
I think your comments about marginal utility are off base. In this case, there isn't a difference between the two.
First, let's consider a case where there *would* be a difference. Suppose I have $40, and I can use that money to buy food and games. I'm very hungry right now, so food has a high utility. But as I buy more food, I start to fill up, and food loses its utility. We'll say
MarginalUtility($1 of food) = 40 - (dollars already spent on food).
Similarly, I get bored playing games, but not as quickly:
MarginalUtility($1 of games) = 30 - 1/2 * (dollars already spent on games).
In this case, my utility is maximized if I buy $20 of food and $20 of games, because that makes MarginalUtility(food) = MarginalUtility(games) = 20. On the other hand, the average utility of the food I've bought is 30, while the average utility of the games is only 25.
Notice that this example depended on food and games having DECREASING MARGINAL UTILITY. But when choosing football plays, marginal utility is constant. A 5-yard gain from passing is equivalent to a 5-yard gain from rushing -- it makes no difference whether I've previously passed 100% of the time or 0% of the time. And if marginal utility is constant, it must also be equal to average utility.
Thanks,
- Nate
Yes, I'll post all curves for 2nd and 3rd down. I'll have graphs and tables of the actual numbers.
Andy, Jim, I think your comments about marginal utility are off base. In this case, there isn't a difference between the two...
Minor point: I'm not talking about marginal utility to consumers but marginal return on investment to producers.
Notice that this example depended on food and games having DECREASING MARGINAL UTILITY. But when choosing football plays, marginal utility is constant.
But Brian's analysis seems to assume the opposite.
He says teams don't pass enough and run too much because return from passing is far higher than return from running. And that the objective should be to pass more and run less until the returns from passing and running equalize.
Yet the only way they can equalize is if there are decreasing marginal returns to passing (and running as well, so that by running less the marginal return of the last run increases).
If the returns to additional passing and running are fixed, they will never change and can never equalize.
If there are decreasing marginal returns to passing (and running) then passing more and running less can indeed equalize the returns.
But with decreasing marginal returns to passing then the average return from passing should be significantly higher than marginal return from passing when the happy equalization point for marginal returns from both passing and running is reached.
Which is consistent with what we see in his data. Or maybe I should just say "not inconsistent", as I'm not making any argument at all about what reality is here, and haven't particularly thought about it. I'm just mentioning a point of logic that should be considered.
Jim,
there are decreasing marginal returns to passing (and running) because they allow the defense to focus in on one type of play, but they apply to all plays, not just one marginal one, because defensive coordinators have the marginal probability of a pass or run in mind for *every* play.
Play calls must be considered randomized mixed strategies rather than subsequent and independent investment decisions. Everyone knows that the Colts throw more often than not (they have a certain randomized strategy, say 70%,30%), so defenses play pass defense sets more often. This should affect *all* of the Colts passes and bring their average return down.
Edward Lee, exactly, the other coach *knowing that passes have higher EV* should immediately stop passes from having higher EV as the coach adjusts his defense to focus on the pass.
Here's a more practical example (using yards instead of EV here, but the results are the same if EV is used):
Let's assume a team's passing offense is slightly better than its running offense: Running plays have average 2y against a run-defense and 4y against a pass-defense. Passing plays have an average 3y against a pass-defense and 6y against a run-defense.
Now for the opposing coach in this situation it is optimal to play run-defense (r) 20% of the time (because the passing offense is better) , which equalises the return from running and passing.
2*r + 4*(1-r) = 3*(1-r) + 6*r
2r +4 -4r = 3 -3r +6r
-2r+4=3+3r
1 = 5 p
1/5 = p
Running plays: 2*1/5 + 4 * 4/5 = 0.4 + 3.2 = 3.6
Passing plays: 3*4/5 + 6 * 1/5 = 2.4 + 1.2 = 3.6
If he plays run defense more often he gets torched by the pass, if he plays pass defense more often he gets torched by the run. Playing this mixed defensive strategy, the defensive coordinator makes the offense indifferent between running and passing.
Similarly, the offensive coordinator can make the defense indifferent between playing pass and run defense by throwing the ball (p) only 40% of the time:
6*p + 2*(1-p) = 3*p + 4*(1-p)
6p + 2 – 2p = 3p + 4 – 4p
4p + 2 = -1p + 4
5p = 2
p= 2/5
Run defense: 6*2/5 + 2*3/5 = 2.4 + 1.2 = 3.6
Pass defense: 3*2/5 + 4*3/5 = 1.2 + 2.4 = 3.6
If the offense throws the ball more often it will allow the defensive coordinator to a pure pass defense, if they run more often, it will allow the defensive coordinator to switch to a pure run defense.
Neither the offense nor the defense can improve on these mixed strategies. Most notably, these mixed strategies should lead to equal net returns of the pass and the run. Higher effectiveness of the pass offense should be countered by coaches playing more pass defense.
This suggests that fault is really with defensive coordinators, who should be playing more pass defense until pass and run become equally effective. Given this unbalanced situation however, offensive coordinators should also choose to exploit defenses by throwing more until the defense fixes its strategy.
Simon: I'm generally sympathetic to the view that marginal=average in the NFL context. But there are some assumptions in the game theory model that may not fully apply in sports settings, perhaps even football.
One is the assumption that both sides are blind when making their play choice. That doesn't seem completely true in football: OCs and QBs may have the choice of passing, for example, when they see something that improves the chance of passing success (or reduces effectiveness of run). In that case, we can't assume that additional pass plays will be as effective as prior ones (separate from whether defense changes it's strategy mix).
I think this is definitely a factor in the NBA. Game theory would tell us the Cavs should score at the same rate when LeBron shoots as when any other player takes the shot. Since this isn't true, LeBron should presumably shoot MUCH more often until equilibrium is reached. It just isn't plausible that the best NBA players, who already take far more shots than other players, should actually be taking far more shots. And in fact there's good evidence that when lesser players are forced to shoot more often, their production drops rather than rises. In the NBA, marginal does not equal average.
Second is the assumption of a continuous strategy mix in which the defense can play pass 40%, or 41%, or 42%, etc. What if that isn't true? What if there is a certain level of pass anticipation possible under the rules, but the only way to further strengthen the pass defense is a large shift of relocating an entire player? There could be a large discontinuity, in which strengthening my pass defense requires a large reduction in run defense. Again, that would mean that marginal changes will not equal average changes.
Guy- Excellent point above.
What do you think of the possibility that the NFL may be at a point where the downfield pass is a dominant strategy (in game theory terms)? That is to say, even if a team passed 100% of the time, and defenses knew to expect only passes, it would still have a higher long-run payoff.
Couple of quick points:
1) Shouldn't a running play almost always have a negative EP, since the avg play (between the 20's) in the nfl gains more yards than the avg run ? In other words, using averages, isn't it pretty much expected that the pass is always the superior option ?
2) Marginal utility is the right call, not averages. If you call so many passes (say 3/4 of all 1st down plays) that the defense always has their dime package on the field on first down, you've probably called too many passes, unless your run plays are AMAZING. Marginal utility takes that into consideration, average does not.
Brian: I was thinking about that idea. To follow Simon's model, what if the average passing gain against a pass defense is as high or higher than the run gain against the pass defense? There's no reason in theory that couldn't be true. But if it were, you'd expect teams to pass more and more until offense became so passing-dominated that the league made rule changes to restore balance. So if it is true, we're looking at a massive inefficiency. I guess I'm skeptical.
(And of course, yards gained isn't the same as EP. The higher probability of a gain that leads to conversion will make running more valuable in some situations, even if expected yardage is lower.)
Another reason marginal may not equal average is personnel -- all players are not interchangeable parts, and they have physical limits. Asking your best receivers to run more plays in a game may reduce their effectiveness. So passing more may require using less talented receivers, which will also reduce effectiveness. (Of course, this could be true of running as well, but perhaps not equally so.)
*
I wonder if there's a way for you to validate the inefficiency without relying on EP. For example, suppose you looked separately at all 1st/10 passes and 1st/10 runs, starting from 25-40 yard line, and measured the outcomes after the down sequences and the possessions. Do the passes lead to more 1st-down conversions? More yard gains on those downs? More points and/or better field position at end of possession? If the EP analysis is correct, some or all of these should be true. (Controlling for overall offensive ability of the two pools, if there's any difference.)
Guy,
You say: "Game theory would tell us the Cavs should score at the same rate when LeBron shoots as when any other player takes the shot."
That's most certainly not the case. Game theory tells us that every *offensive strategy* should score at the same rate, but a single offensive strategy can result in many players potentially taking a shot.
For example, one strategy might look like "LeBron attempts to drive to the hoop for a layup. If that doesn't work, he passes to someone else for an outside shot." With that strategy, LeBron would shoot a high percentage and the rest of the team would shoot a low percentage. But that certainly doesn't imply that LeBron should also shoot when the drive to the hoop fails.
Essentially, the difference boils down to the fact that a basketball player can estimate the probability of making a shot before deciding whether to shoot. In football, on the other hand, the hypothesis is that the offense does not get a chance to react to the defense before choosing a play.
Thanks,
- Nate
Guy:
"How is it that both runs and passes have positive value within the 20? I would have thought the combined EP of all plays was zero, but obviously not."
Not sure why that assumption would be made. I think if Brian ran the numbers, *any* play on 1st and 10 within the 20's would have positive EP, and that positive EP would be averaged somewhere between the value of run(EP) and pass(EP) for that yardage.
I think the simple answer is that the offense, in general, runs a positive-EP play on 1st and 10. This may be untrue, as penalties and other things are removed from the equation. But I think that it's unlikely that the average result of 1st and 10 plays is to reduce EP. Therefore, it is entirely consistent that run(EP) and pass(EP) do not combine to zero, but rather combine to a positive EP value.
Brian,
"What do you think of the possibility that the NFL may be at a point where the downfield pass is a dominant strategy (in game theory terms)? That is to say, even if a team passed 100% of the time, and defenses knew to expect only passes, it would still have a higher long-run payoff."
This is the case quite frequently in college football, but the opposite direction. You have successful teams that are almost exclusively running teams Georgia Tech at 83%, almost 85% on 1st down. Surprisingly, the highest percentage-passing team I could find with a good record is Houston at 63% passing, and then only 59% on 1st down.
But the key is that for a team like Georgia Tech, you know they're running at you 83% of the time, you're defending primarily the run, and yet they're a 10-1 team leading their division. It's simply the fact that opposing teams do not have the personnel packages to match the offense.
It was the same thing in the Big Ten, as I'm a Purdue fan, back in the late 1990s. When Joe Tiller came into a conference known for (3 yards and a cloud of dust) with a spread offense, opposing defenses didn't have the personnel packages to match up. We were able to get WR's covered by slower run-stopping LB's, and the mismatches generated allowed us to pass despite the fact that our opponents were expecting the pass.
You see something similar from the Saints right now. With Brees behind center, some big talented receivers, and a wide-open spread offense, they are able to create mismatches. While a conventional pro-style offense would allow opposing defenses to double-team Marques Colston, they go 4-wide with an RB. Opposing teams can't double-team Colston AND also be able to adequately cover the other receivers AND stop the run or HB outlet-pass.
Will the NFL ever reach a point where it's a 100% passing league? No, because opposing defenses will obtain the personnel and practice time necessary to defend a 100% pass offense. You'd see every team playing a dime defense on every down, making them too susceptible to the run for an offense to try to stick to a 100% pass offense.
Finally, the question was brought up as to marginal value.
I figure marginal value of increasing passes should be considered as a percentage matter. As Brian shows, offenses between the 20's are running, on average, maybe 52-54% of the time.
So one discussion of marginal value would be on any given pass play, if the EP is greater for a pass, one would think that the coach should choose to pass. And thus would extrapolate that the coach should choose to do so on the next 1st and 10, and the 1st and 10 after that, and so on in perpetuity. But as Brian points out at the end of his post, these numbers are purely for the NFL on average, not a given team. If one coach decided that due to Brian's post, he was always going to throw on 1st and 10, he might get through a half, or a game, or even two games before opposing defensive coordinators caught on and started adjusting their defenses.
Ideally you need an offense where the defense has to respect both run and pass on 1st and 10. To do so they need to know that you're likely to do either. Brian postulates here that the magic number is the 53% run / 47% pass that is prevalent in the league. Maybe it's 56% pass, 44% run. Maybe it's higher, 62% pass and 38% run.
But at some percentage run/pass mix, opposing defensive coordinators start putting in nickel packages on first down, making running easier and passing harder. AT THAT POINT, the marginal value of passing more becomes negative.
How does an offensive coach then decide whether to run or pass on 1st and 10? However he wants, as long as he mixes in the percentages such that he's averaging out to the level of runs vs passes that have the best EP per the statistics.
Jim, there are decreasing marginal returns to passing (and running) because they allow the defense to focus in on one type of play, but they apply to all plays, not just one marginal one...
I know the argument and mentioned it (briefly) in my first comment. But it is not as obvious as it may seem.
For one thing, saying "marginal = average" means in a single game it is impossible to pass too much -- because, as marginal = average, the marginal return never drops below the average with additional passes, so return to passing is constant in each game.
Do you really believe that? As an anecdote, FOers on last week's Panthers game:
"Why did they have Jake Delhomme drop back to pass 44 times? He threw 16 times on first down -- 16 times! Predictably, they resulted in six completions, 78 yards, and four first downs. They only ran the ball 15 times on first down, and while they got 66 yards, they put the team in far better situations than Delhomme's 10 incompletions."
OK, anecdote does not equal data, this is just some guys opinion, but we also have the disappearance of the run-and-shoot after a concerted test (except as absorbed into more conventional offenses).
If a team can pass (or run) too much in a game, then marginal returns must apply within it (run-and-shoot Houston blowing a 32-point playoff game lead to Buffalo is another anecdote) -- and marginal does not = average in individual games.
The disappearance of the run-and-shoot points to a larger issue -- which I'll put in another comment (since this keeps getting rejected with a strange error code when it's included in this one, in spite of being under the length.)
Nate: I think we're saying the same thing. If the Cavs had no opportunity to evaluate the defensive position and LeBron's chance of success before deciding whether he should shoot -- which is the assumption in most game theory examples I'm familiar with -- then he should shoot more often until the "LeBron strategy" is equally effective as having any other player shoot. But obviously, in basketball the offense has a lot of information before they have to make that decision. (It would be like if QBs still had an effective run option after spending several seconds looking for an open receiver.)
Brad: The average EP must be zero at any given down/yard/field situation. EP before the play is the expected points given the average of all future outcomes. One play later, the average EP must therefore be the same, by definition. Look at it this way: if initial EP is 1.0, and then the average EP one play later has become 1.1, then your initial EP estimate was wrong!
Where was I? Yes...
The disappearance of the run-and-shoot (except as absorbed for situational use into more conventional offenses) points to a larger issue:
As the old saying goes, "Extraordinary claims require extraordinary rationales/ explanations/ something to support them".
The argument that passing is so much more effective than rushing -- rushing is so often is negative! -- is far stronger than the claim "coaches punt too often on 4th down", which relates to a much smaller part of the game and is easy to explain.
"Coaches are ignorant and/or intimidated by fans and commentators out of passing more" doesn't work, because scads of coaches have used big-time passing attacks, and fans and commentators love them.
If anything, owners and pundits have put pressure on coaches to pass more. (See the creation of the old AFL and the changing of the passing rules in 1978.)
So how to explain the "dearth" of passing nonetheless? If passing is so underused, why have attempts to use a lot more of it failed? A credible explanation is required.
One possibility, as noted, is average return exceeds marginal return.
But another possibility that could preserve "average = marginal" is standard economics too: structural inefficiency, as touched on in a prior comment.
It's well known (especially today!) that resource allocations can systematically "mis-set" because pricing doesn't work instantly and magically at 100% efficiency through the aether, but with finite time lags through structured institutions, legal rules, etc, that can impose systematic bias.
Maybe the rules of football are just biased structurally to produce the result seen. By how the players must line up, something, I dunno.
In the simplest case, there just may not be enough plays in a game to pass enough to reduce the return from it.
There are situations where running is best: short-yardage, draw plays to slow a pass rush, setting up play action, to keep the defense rested (remember Buddy Ryan punching out Gilbride on the sidelines over his "chuck-and-duck", er, run-and- shoot offense), control the clock, etc.
Given the 65 or so plays a team gets in a game, after running the amount of times when it is best to do so there may not be enough chances to pass remaining.
OK, using first down, early-game data is supposed to reduce these considerations. But we have to start developing our ideas somewhere.
And really, an explanation for this massive inefficiency does seem needed given how Air Coryell and the run-and-shooters and so many other have tried to close it.
If the explanation is neither "average return exceeds marginal" nor "structural inefficiency" then for the moment I'm at a loss as to what it might be.
A couple things. Guy is correct about the average EP being zero. If it's not zero, then the 'Expected' part of Expected Points must be wrong. I'm fairly certain the reason for the non-zero average is that there are plays that are not classified as either runs or passes, and they are almost universally negative outcomes for the offense. These plays occur more frequently near the goal line.
Regarding the debate between average and marginal utility. I think I understand the disconnect now. Essentially, we are all correct. Marginal utility is another way of expressing the whole notion of zero-sum game theory. I think some of us are more game theory-oriented and some of us are market economics-oriented.
Zero-sum game theory itself relies on the fact that the utilities of various strategies vary as a function of how frequently they are employed, assuming the opponent has a counter-strategy. The more you rely on one strategy, the more it will be countered, and the lower its payoff.
Whether we call it marginal utility or think of it in pure game theory terms, the prescriptive solution is the same. The point at which the long-run utility is maximized occurs when the strategy mix results in equal average utilities for each strategy. This is the 'minimax,' or Nash equilibrium. If they aren't equal, then the strategy mix is not optimum.
"If they aren't equal, then the strategy mix is not optimum."
OK. But one thing to consider is that the Nash equilibrium should exist at the team level, not the league level. Or even more specifically, should exist for any given offense against a given defense. So there is no guarantee this will produce equal EP for the run and the pass league-wide. If better offensive teams tend to pass more frequently on first down, then the average NFL pass could have a higher EP than the average run while every team was still in equilibrium.
But think about the logic of this theory. Equilibrium means that every single team should have equal EP for its pass and run plays, at any given down/yard situation. So if you ranked the 32 teams in terms of run EP and pass EP, the two rankings should always be identical. A team with a great QB and receivers and the league's worst RBs will just keep passing until the two strategies are equally effective; a great running team with a weak rookie QB will do the reverse. There really should never be such a thing as a team that's significantly better when running or throwing, only teams that do them in different ratios.
That's what game theory requires. Brian: does that seem like a realistic model of how the NFL works? Or could work?
I agree. And to go a step further (back), it's not just that individual teams should be at different equilibria, but that each team should be at a different equilibrium against particular opponents.
There is certainly a good deal of bias in these numbers, as I said in the article. Teams that are good in passing will tend to pass more often, so that there are extra cases of the better passing teams in the sample. That's why I'm not claiming that "passes add exactly X expected points to a drive."
That said, the reverse is also true. Teams good at running will tend to run more often, biasing those numbers too. The fact that the 'EP Added' for passes is higher than that for running, and not the other way around, is evidence teams are running too frequently as a whole. How much, I don't know.
Further, if correct, I believe this is instructive about how to build a team. GMs should build teams good at passing rather than good at running. This is consistent with other research that shows (very clearly) that being good at passing correlates with season wins much better than being good at running.
Of course, "draft a Peyton Manning" is easier said than done.
Guy-By the way, I have a lot of great commenters here, and I learn a lot from all of them. But I have to admit no one teaches me more or makes me re-think my assumptions as well as you. I see your comments at other sites too. You're like the designated thesis advisor for sports analytics sites. Thanks. You should have your own site!
Guy,
Okay, I think I understand why my interpretation of EP was wrong... And I think I understand where the confusion came in for you as well.
If you look at the graph, I don't think it's a graph of EP at any given field position (which, as you point out, should average to zero). It looks rather to be a graph of EP Added based on the play called.
So a graph of EP would (likely, I'm just hypothesizing here) be sharply negative within a team's own ten yard line, tend up to cross zero somewhere near midfield, and improve markedly as you approach the opponent's goal line.
So if you've got 1st and 10 at your own 20 yard line, your EP might be -2.10 (as a rough guess). If you pass, and the average pass nets 7 yards, you now have a 2nd and 3 from the 27 which for argument's sake has an EP of -1.95 (consistent with the 0.15 EP added of a pass from the 20). If instead you run, and get an average of 4 ypc, you now have 2nd and 6 from the 24, which (according to the chart posted) actually hurt your EP when you consider down/distance in addition to field position), for an EP adder of -0.02, and a new EP of -2.12.
I.e. controlling for 1st and 10, EP rather steadily increases across the length of the field. At any given yardage (i.e. 2nd and 1 at your own 32 vs 2nd and 14 and your own 32), down and distance changes the EP value. So if you start at one down/distance and favorably improve your down/distance as well as field position, you add to EP. If you don't favorably improve your down/distance & field position (i.e. the negative EP of 2nd and 7 may have negated any positive effect you had of gaining 3 yards of field position), your EP can hold constant or drop.
I think this explains why Brian's graph doesn't average to zero. If he graphed EP (rather than EP adder of play call) of 1st and 10 across all yardages, it should average to zero though.
Brian, would you agree? And would you mind posting a link to your original EP article? As a fan of football, economics, and an engineer, I think I've just found a blog that I will be reading regularly :-)
How far-fetched is it to throw on every down in the NFL?
Let me clarify: The average NFL completion is over ten yards and completion percentages hover around 60%. In its most crude form, that would imply just a 6.4% failure to convert a first down. Now, OBVIOUSLY some completions (or just above half) should result in plays under ten yards, OBVIOUSLY teams would play to counter the pass, and OBVIOUSLY there are negative pass plays (sacks, fumbles, INT) that would either lose possession or create a situation where a ten-yard completion wouldn't convert.
But if you threw every first and second down, converting on those two plays should occur pretty often with a lot of 2nd or 3rd & short situations. This is where the strength of running comes into play, since it has such a thin peak in its probability distribution.
Furthermore, running this type of offense solely out of a no-huddle would either make those short-yardage situations a lot easier to convert (if the defense chose pass heavy personel) or keep a favorable passing scenario (if the defense chose its base defense).
This all not to mention the fact that, if this offense could run successfully, it'd be using less clock than a typical offense...thus extending the number of possessions in the game, meaning the randomness of the game decreases, ie. this team wins more often than another team that scores on its possessions the same percentage that this team scores on its possessions.
Of course this is a very, very crude exercise, but I'd be willing to bet this basic model for running an NFL offense would be more successful than any team currently in the top half of first-down running attempts (in non-clock related scenarios).
"Okay, I think I understand why my interpretation of EP was wrong... And I think I understand where the confusion came in for you as well."
Brad: I wasn't confused -- all plays should average to zero. When I talked about run and pass "EP" I meant the EP added, which is what Brian is discussing here. It's an important distinction, though, and maybe calling the net change per play "EPA" would be more clear. I think your explanation is correct, except when you conclude that "if he graphed EP (rather than EP added)... it should average to zero though." It's the other way around: EP will vary by field position and down/yards, but the average EPA for plays at any given starting point will always equal zero.
Brian: Thanks. Maybe I'll start a blog some day, but kibbitzing is so much easier!
I don't disagree that the evidence points toward "not enough passing." That may be true. Though I'd be surprised if it's as large as your chart here suggests -- a spread of about .15 points per play seems huge to me.
And maybe for some teams, facing some defenses, passing is now a dominant strategy except for short yardage plays. Perhaps the Colts should pass 80% against some opponents*, or whatever the constraint is imposed by physical limits of their best receivers.
On the other hand, I think football is just a lot more "sticky" than game theory. Game theory tells us that every team will be exactly as effective when running as when throwing (and every defense equally accomplished in both areas). There would be no such thing as a good passing team, just good offensive teams (who would always be equally good on both pass and run, relative to league average). Even if every GM and coach read this blog and understood game theory, I'm not sure this is a plausible model of reality.
And I'm still unsure that EP can entirely answer this, though it's a very powerful tool. The problem is that it's based on what teams will actually do in the future. So it's somewhat circular: it's trying to establish the right pass/run mix, but it assumes the current mix on all future plays. If a 9-yard gain on 1st down invariably leads to a conversion, that gain is highly valued in part because EP "knows" that teams can then run for a 1st down. A deep pass attempt on 2nd down is then a low-risk/high-upside move, but only because a 3rd-down run is a safe fallback option. And if a short run does convert on 3rd/1, the EPA is low (I assume). It seems like the low variance of the run play may not get its due, because EP already assumes it will do its job when needed. But, I may well be thinking about this incorrectly.
* In your post on how a great RB would effect run/pass mix, you conclude there should be no effect. However, you assume that the great RB improves each run option by a fixed amount (1 yard). Isn't it more plausible that the gain is proportional, say increasing yardage by 25% against each defensive strategy? And if so, wouldn't that mean the offense should in fact run more often?
Excellent work.
And they say Andy Reid passes too much...ha
I should point out that the other 2 studies I mentioned above used a regression to try to eliminate the bias we've discussed. They use dummy variables for team-years to account for varying team strength in running and passing.
Jim-There are a number of possible explanations off the top of my head.
1. Coaching is too slow to adapt to the new reality of passing supremacy. Today's coaches learned their football in the 70s or 80s from other coaches who learned it in the 50s and 60s. Running a lot made more sense back then.
2. The Ellsberg Paradox, which I wrote about previously. There is a well-known heuristic bias where people prefer a certainty to a less-certain, but net preferable alternative.
3. Coaches fall prey to the run-win causation fallacy. (Which we know they do, if you listen to former coaches who become analysts.) They see teams with high run to pass ratios have good records, so they target a certain ratio. 1st down is really the only opportunity they have full latitude to select run or pass because subsequent down/distance situations often dictate a certain type of play.
I think reason #1 is the most plausible theory (of course, could be more than one cause).
Could coaches have a rational reason to want to minimize the risk of running 3 plays and punting, especially early in a possession, because of the impact on the defensive squad (forcing them back on the field so quickly)? If running on 1st down increased the likelihood of achieving a first down, but at cost of worse average field position, could it sometimes be the correct move? (Assuming it does increase odds of 1st down.) Just thinking aloud here....
Jim - There are a number of possible explanations off the top of my head.
Coaching is too slow to adapt to the new reality of passing supremacy ... The Ellsberg Paradox ...Coaches fall prey to the run-win causation fallacy
Well, the coaches and owners who brought the run-and-shoot to the league, and proselytized it (as they did -- they certainly weren't adverse to the idea of passing supremecy), wouldn't seem to have been held back by such things. They're still around. Why'd they give it up?
My point here is that there isn't the natural bias against "more passing" in the NFL that there is against "going for it on 4th", or that there is in "Moneyball"-type situations against underarm throwers and fat, slow first basemen -- which require a James to analytically prove, and a Beane to then show that underarm throwers can pitch and fat, slow first basemen with high OBP can have more value than lean, mean athletes, contrary to all "common sense".
There's always been bias in favor of passing in pro football. The owners have repeatedly changed the rules to promote more passing. The AFL was created as a passing league, and those owners and coaches came into the league. Owners and coaches have brought in and marketed the run-and-shoot, Air Coryell, the Greatest Show on Turf (updated Air Coryell), and the fans have loved it. Since the days of Don Hutson, every generation of pro football has had its "record setting passing heros" ... which is pretty inconsistent with a universal bias against passing, either for the purpose of winning games or selling tickets, which is the sort of universal bias-based inefficiency we see in the other cases.
So it's hard for me to see institutionalized or psychological resistance causing passing to be greatly underutilized -- not comparably to the other cases.
Another oddity is that when inefficiencies are exposed, the new successful practice tends to spread quickly and the old prejudices evaporate. Once the Dodgers signed Jackie Robinson, the rest of baseball followed. Moneyball analysis really has changed how baseball values players. For all the Belichick brouhaha, teams are going for it on 4th down more than ever before (as he did).
Pro sports are extremely competitive, and the NFL in particular is highly imitative. Whatever succeeded recently gets copied by half the league in short order. Look at the Wildcat. Three years ago, who would've thought the option would be spreading through the NFL like the flu?
But for all the high-power passing attacks and passing advocates there have been in the NFL, and for how the owners favor passing and fans love it, this major under-use of passing persists. Leaving both wins and fan $$$$ on the table. It's strange.
Note -- I'm not arguing, just discussing, thinking out loud. I believe your data.
But I think all this points to interesting issues.
The team-level analysis you mentioned could be really informative here, ISTM. I could suggest a lot of ways to slice that data to illuminate what's going on here -- but it's your data, and you'd do the work, and you're so good at it, I'll leave all those ideas to you. I just hope you see the point I'm trying to make.
Guy said...
Could coaches have a rational reason to want to minimize the risk of running 3 plays and punting, especially early in a possession, because of the impact on the defensive squad ?... Just thinking aloud here....
Being that Buddy Ryan punched out Kevin Glibride in mid game while the latter was calling the run-and-shoot for just that reason -- Buddy's players were collapsing from exhausion -- we can safely say that some coaches think along those lines.
Of course to win the game the team wants to maximize total efficiency, not just offensive efficiency. If improving offensive efficiency in a given way reduces defensive efficiency, then...
It's common for coaches to manage the O to protect the D. Sometimes it works -- when Parcells was in NY he always ran the play clock down to near zero on O-plays to give the D rest. Sometimes it doesn't -- when Herm was coaching here too ... well, best not to think of that. But if a D is the team's comparative strength, it can make sense to play to it smartly.
In the spirit of "thinking out loud", some thoughts relating back to the past discussions here of "yards per play" and the "passing premium".
Passing yields more yards per play on average than rushing over the long run because of the higher risk involved -- picks, sacks, 0-gain incompletions, etc.
Still, one might say that since passing does produce more over the long run, I'll just play for the long run, pass, pass, pass, eat the bad things as they occur, and come out ahead in the end as my reward for being smartly brave and aggressive.
The problem is that in a football game the long run isn't so long and gets shorter every play, and bad things can occur by random chance not spread out over time but together in a big clump -- with your remaining run not long enough to recover from them.
E.g.: Peyton Manning throws six picks against SD. Houston running a run-and-shoot blows a 32-point playoff game lead to Buffalo. Look at the play-by-play for Hou at the end and it reads like: inc, inc, inc, sack, inc, pick, sac, inc, pick, inc, sack ... and that was really a tremendous passing offense in the aggregate all year long. When you incur risk very bad things can happen by dumb luck.
As a result, as Brian explored in detail at the time, just as in financial practice, it can make sense to construct a "portfolio" of plays that reduces passing and the higher average yards per play expected from it to a certain extent to reduce the downside risk involved, with the risk savings more than offsetting the loss of average yards, to an optimal point -- the risk a team can afford to incur varying by the time left in the game, the score, etc.
I've been wondering about how corresponding risk is handled in this EP analysis. I'm sure its considered, as it is hardly an unfamiliar idea on this site. But, e.g, as to:
"For example, a 1st and 10 at midfield is typically worth 2.0 EP. A 2nd and 5 at an opponent's 45 is worth 2.2 EP. So a 5-yard gain on 1st down at midfield would produce +0.2 EP. This method factors in risks such as sacks, fumbles, interceptions, incompletions, penalties, safeties and everything else."
I wonder how the risk is factored in. Are all the "bad things" considered to just produce an average EP value for each play, in which case the situation is analogous to the higher average yards per play we get from passing, and we'd expect a significant passing premium?
Or is the risk considered as in developing portfolio analyis, considering the greater compound risk of a bunch of bad things happening all at once, which methodology we'd expect to largely eliminate the passing premium, but with the big passing premium still mysteriously remaining?
If this has been covered earlier, please forgive, I think I've missed parts of the explanation of EP.
Concern about 3-and-out only makes sense, of course, if the 1st down conversion% is lower when a team runs on 1st down. Perhaps Brian can tell us if that's true.
I think Jim presents a strong case for skepticism about a large inefficiency, despite what the EPA data seems to show. Another angle on this is to see how much variance exists in terms of teams' 1st down pass%. I would guess it's pretty high, and that the teams which pass the most tend to be good passing teams. If so, that makes the inefficiency unlikely, because you will have some teams clearly succeeding more often by passing. Even if coaches/teams don't understand the probabilities, immitation will tend to wipe out the inefficiency over time.
For a large inefficiency to persist, we should observe very low variance, and thus no teams effectively exploiting the inefficiency. That's what we see with 4th down. If everyone follows the CW, then the CW can remain wrong. But that's not the case with passing.
That's why I think it's worth trying to validate this with more traditional metrics: do high 1st down pass% teams convert more often than they should? Score more points? Win more games?
I'm no longer a big believer in the portfolio metrics for football. I think they can help measure which teams are aggressive or conservative, but they cannot be prescriptive.
Financial portfolios are very different from a football game. You don't get to carry forward gains from one game to the next. In other words, you can't take a 20 point lead with you into the next game, like you do with portfolio gains.
The utility curve of monetary gains bends. In other words, the first $100k in savings is more important to me than my next $100k, and far, far more important than my 20th $100k. This gives value to low-variance, low-risk decisions.
Football isn't like that, my fist 10% chance of winning is just as important as my next 10% chance. Win Probability is a perfectly linear utility. And in 'normal' football (as I try to define it-close score, time not a factor), every net point advantage over an opponent is equally valuable.
Also, variance is not necessarily a big concern. In a strict 2-player zero-sum world, I don't care whether I win with highly erratic large swings in gains and losses, or with tiny incremental gains. I only care if I win.
Lastly, the consistency or low-variance value of the run vs the pass is already factored into the EP model. The EP value of any play takes into account the prospective likelihood of converting first downs.
One other note about the run-and-shoot offense. As I understand it, it wasn't about passing a lot on 1st down. It was a specific kind of read-react doctrine for QBs and receivers. It failed because pro defenses quickly learned how to counter it effectively, not to mention that the teams that employed it weren't all that good.
I'll post a bunch of graphs on this in a few days, but here are some initial results. Outside the red zone, passing on 1st down subsequently leads to a conversion 69% of the time. Running on 1st down leads to a conversion 65% of the time. Conversions are what keeps a defense off the field and rested, whether they come from passing or running. Buddy Ryan would be happy.
Yeah, I never saw the value of the portfolio analysis. I value low variance in financial returns because I may really need the money at a particular time. In football, everyone always needs their points at exactly the same time -- at the end of 60 minutes. And the EP and WP metrics incorporate that reality.
The 69% to 65% conversion spread is VERY strong evidence. If passing leads to more conversions and -- I assume -- higher yardage gain, that's obviously a higher EP. My resistance is breaking down! However, a couple of factors remain that might mean the actual inefficiency is smaller than the league numbers would indicate:
1) if better offensive teams pass more often on 1st down (this doesn't appear to be true overall, but may be true in "normal football";
2) if the missing plays -- QB fumbles, penalties before the snap, others? -- are disproportionately coming on planned passes.
But a question for Brian on the larger game theory model: your team run and pass metrics in the team efficiency model have zero correlation this season. If game theory is right, the correlation should be 1 -- a team's run and pass rankings should always be identical (I think). Any thoughts on how that could be?
Brian is completely right about the absurdity of applying portfolio analysis to football WP decisions. The bend in the utility curve is the only reason why you need to bother with things like "risk management", etc. This is a really important topic, because it appears to come up a lot. It seems like people are saying that a stable 75% WP is worth more than a 50% shot at 50% WP, 50% shot at 100% WP. Thats just wrong, even though it is conventional wisdom.
This isn't to say that all football decisions are perfectly linear. On a run, the first yard is worth far more than the 50th. In some cases, the 6 inches immediately in front of the first down marker can be worth >30 yards. But all of this is accounted for in WP already.
I'm amazed at how many conventional football people are willing to spout cliches like "winning is the only thing" but not actually use that principle in their decision making.
So a low variation decision that leads to the same expected win percent is equal to the high variation decision in a small sample?
Brain:
As you may no I came to your cuntry through cadana. Does your 1st down theereys work fo the Ligue of the Cadana Football teems? - yes.
If so do you like the Rough Riders or the Roughriders.
PS I support your war of terror!
May I make a suggestion? Before I begin, let me say that your conclusion is in line with my feeling on the subject, but I think that analyzing the value of certainty would be helpful. If your data set allows it, I believe that I can suggest a potentially interesting avenue of investigation.
For each 'bucket' of field position, for both runs and passes, evaluate the following:
* Run a distribution of results (i.e., X1% of Y1 yards gained, X2% of Y2 yards gained, etc.)
* Evaluate the +/- for each result and then evaluate the full distribution - because the value of +/- 1 yards is almost certainly not linear with respect to yards gained/lost.
* Take the weighted average of these distributions.
I believe that these results will yield a similar conclusion in a much more persuasive manner with respect to the value of uncertainty.
-------
Secondly, while this analysis is meaningful for the value of a current drive and the next drive, it does not evaluate something that the coach likely holds dear - long, clock-grinding 'body-blow' drives meant to tire the opposition. If the entire analysis (with the above change in methods!) were repeated with respect to likelihood of getting an additional first down (or touchdown if inside the 10 yard line), that mightly more closely model the actual goals of 1st and 3rd quarter coaching goals.
-------
Finally - is your data set available in excel? I'd love to play with this myself if possible.
Brian--
This is another good article and I usually agree with you, but I think you are greatly underestimating the importance of having a balanced offense. By isolating individual plays to compare their EP values, you are overlooking the interdependency of all plays, which is pretty much the essence of play-calling. I'm guessing the average EP of passing plays is heavily weighted by long TD passes that were made possible by the fact that the defense was expecting a run. You might argue the converse is also true, but most people will agree that run/pass interdependency is not entirely mutual. For example, the more a team stacks the box to defend the run, the more susceptible it is to long TD passes. But the converse is not true; when a team is playing prevent pass defense, it is not more susceptible to long TD runs--just a bunch of 8-12 yard runs. This is a subtlety of the game you simply can't put into numbers, as much as i'd like you to. Keep up the good work.
Brett- Long TD passes count, don't they? Otherwise, we completely agree. My point is that teams are running too often to constrain defenses to the run. And each time they do, they're actually sacrificing optimum performance. The interdependency of playcalling is exactly what the game theory model is for.
We sure can put those subtleties into numbers. It's just a matter of how detailed our data is.
Brian- I agree that each time a team runs on 1st down, they are sacrificing optimum performance...on that play. But they are setting up those long TD passes to a degree we cannot measure. Can two 1-yard runs cause a 90-yard TD pass? Would that 90-yard pass have happened anyways without the run plays? I don't think these questions can be answered by the game theory model. This is why I believe measuring the success of a single play is not an appropriate method of judging the full-game chess match that is play-calling.
If we agree that in 'normal' situations that net point advantage is all that matters, and that every point is equally valuable, then that's exactly what I'm saying. Teams are running more often than necessary to set up those longer passes. If what matters is overall, long-run net point maximization, then teams should generally run less often.
There is nothing controversial or debatable about that.
"Teams are running more often than necessary to set up those longer passes."
Without knowing
1) which specific runs are intended to be set-up plays
2) which specific passes are follow-up plays
3) how the results of the follow-up plays would change based on the number of set-up plays
I don't see how you can possibly justify that statement.
"If what matters is overall, long-run net point maximization"
... *per play*. Per-play net point maximization may not be the same as per-game net point maximization if the outcome of a play depends on prior plays after accounting for field position, down, distance, etc.
Pat-You still seem hung up on sequence. "Follow-up" plays and preceeding passes are irrelevant. I don't need to call a run first to get you "set up" for a pass on the next play. I just need to have you aware that I'll call a run with some probability on the current play.
Chris Brown (of smartfootball.com) once wrote that play calling in football is not much different than rock-paper-scissors. Say I plan to play rock, hoping you'll play scissors. I don't need to play paper on a preceeding instance to set you up for scissors. You just need to be on guard against the possibility I might play scissors now.
I'm guessing coaches think like you do, believing they need to run first, and that might help explain why they run too often.
Deliberate sequencing is a very bad idea for an offense. It creates a pattern, which however slight makes an offense predictable to some degree.
"I don't need to call a run first to get you "set up" for a pass on the next play."
I don't see how you can claim this with absolute certainty when coaches have *flat out stated* they call plays in order to see how a defense reacts. Calling a 'test play' to see how a defense reacts is the same thing as 'setting up' a defense, just using different terms - in that case, the offense's "follow-up play" is determined by the defense's reaction to the first play, rather than the defense's reaction to the follow-up play being determined by the first play.
You're also only thinking about it from the defensive playcaller's point of view, and *not* the defensive *player's* point of view. A defender has to react to what he sees, not what *could* happen. His reaction time is going to be modified by what he knows about the team, and what he's seen that game.
"Chris Brown (of smartfootball.com) once wrote that play calling in football is not much different than rock-paper-scissors."
In terms of the offensive coordinator/defensive playcalling matchup, yes. But that's not all that's going on. Defenders reactions can be manipulated, personnel groupings on the field can be manipulated, etc.
And you can't follow a mixed strategy with either play reactions (since it's 11 different decisions - 11 random actions wouldn't work well) or personnel groupings (since the defense doesn't have completely free substitution and doesn't know what the offensive formation is).
Chris is also a (self-stated) option purist - and the entire idea of an option is the fact that you can react to what a defense does. Which means that the *next* time, the same play's outcome depends on the previous play's outcome as well.
A good example is back when Chris described the inverted veer option from TCU: here. When a formation shifted, the defense reacted based on a previous formation they'd seen on film, and it completely crossed them up.
"I'm guessing coaches think like you do, believing they need to run first, and that might help explain why they run too often."
What I'm confused at is to how you can state with a certainty that they *don't*. There's no theoretical reason why the success of pass plays couldn't be entirely set up by leading the reaction of the defense.
We *know* it's possible to manipulate a defense's reaction based on things that occur during the play. That's what QBs do when they move DBs with pump fakes and look-offs. All this is saying is that early-play action can also manipulate a defense's reaction.
"Deliberate sequencing is a very bad idea for an offense. It creates a pattern, which however slight makes an offense predictable to some degree."
Of course the defensive players could try to predict it. But the problem is that they have a grand total of a half of a second to predict it. The defensive playcaller can say "on this play, look out for C, because they ran A earlier" but a defender still has to recognize the difference between A and C, and whether or not he is *capable* of doing that is a matter of skill, not game theory.
Maybe coaches shouldn't be so cavalier about 'test plays.'
Option plays, of any kind, will nicely collapse into a sub-game at the parent node of the general play type (run or pass).
"Maybe coaches shouldn't be so cavalier about 'test plays.'"
I don't understand this comment. You have no idea how much value they result in, since you don't know what plays were "test" and what plays were changed due to that "test."
It's relatively easy to test your assertion that teams should run less: group teams by run/pass percentage on first down in 1st/3rd quarters, and plot average total EP/drive for all drives in those quarters.
If it's true that teams should pass more on first down, the teams that *do* pass more on first down should be doing better than those that *don't*.
"Option plays, of any kind, will nicely collapse into a sub-game at the parent node of the general play type (run or pass)."
Play 1: Offense notes that defender crashes down on a certain type of run - OC adds a run option, which allows a pitch-out if that defender does, otherwise a keep.
Play 2 (not necessarily next): Offense runs previous play - defender repeats previous action, and offense gets a big gain.
Play 3 (not necessarily next): Offense repeats previous play, defender adapts (playing better gap discipline, etc) and play results in a minimal gain.
Play 4 (not necessarily next): Offense repeats first play, defender plays as before, play results in a decent gain.
Those plays depend on the previous history in the game. If play 1/4 average (together) less than play 2/3 average (together), you might ask "why don't you run play 2/3 more often?" and the reason is because play 2 (the big gain) only occurred because of what was noticed on play 1, and by play 4, the defense had adapted to play 2/3.
You might think that this would trend towards an equilibrium, and it could - but that equilibrium may not be at the minimax point, and that equilibrium probably wouldn't be reached in a 60-play game anyway.
Didn't read the whole thing because I have a headache, so if my critique was addressed, then please just say so.
Anyways, suppose you are right that NFL offenses run too much on first down. Does that take into account that perhaps some teams are just better at running than passing and are playing to their strengths? Take for example, a team with a rookie QB. That team will likely run a lot more than pass.
The defense may game plan for the run, which under normal circumstances, make it smart for the offense to pass. But given that the offense has a rookie QB, and the expected outcome from passing, even given a run-oriented defense, may be only slightly higher than running the ball, then perhaps a team may run more than pass.
Basically, you may be right the NFL as a whole runs too much, but on a team vs. team basis, matchups actually dictate what is happening.
Brian, I am new to the site, fantastic stuff.
Another "set-up" thought: Running takes a toll on the d-line. Passing takes a toll on the o-line.
Can you see this in the data? For example, do teams who have executed more running plays (not a higher % of running plays, but I higher number of running plays) in Q1 and Q3 have more offensive success in the 2nd and 4th quarters?
Running on 1st is an investment for future gains in the 4th quarter. Everyone knows that running is most effective in the 4th quarter.
Moreover, the risks of passing go up with more passes, and the single most important factor in the NFL is turnovers.
Question: When a QB fumbles, is that considered a running play? If so, this would throw off the stats big time.
Do you factor in whether the other team's offense is better than yours. Much like teams that play against Peyton Manning or Tom Brady, sometimes the best way to defend those guys is to take time off the clock and shorten the game. A 3-and-out running the ball takes at least 2 more minutes off the clock then 3 incomplete passes.
Also, how do you account using the run to set-up the run in the 4th quarter? A lot of coaches say the only way to insure you run the ball when you need to in the 4th is by banging away and weakening the defense in the first half. By limiting the analysis to just those plays when "neither score nor time is important," have you factored that out?
Hi,
Sorry to post a comment years later, but I was directed here via deadspin. After reading some of the comments, it seems that some of the people arguing over average v. marginal utility are using odd models of game theory (or just don't really get how one accomplishes figuring out maximizing overall utility). I think all of the arguments stem from some version of a model where a team that runs 100% of the time and then suddenly passes would benefit greatly from that pass. From an individual play standpoint, sure, doing the thing that maximizes utility would be the proper move if the game were only played on one iteration. But for a multi-iteration game, they're essentially implying that the reward values in the matrix will not be constant amounts but will be frequency dependent. And that's fine; the calculus to find the Nash equilibrium becomes a little more complicated with multiple references to the frequencies in the equations, but there is still a Nash equilibrium. And as you correctly point out, the equilibrium stabilizes the per play value (and should therefore render the average pass and run plays equivalent), though it may be outside of the proper frequency ranges, of course.
Regardless, I think what you're really identifying in this article is that they are not at the Nash equilibrium, and the way to drive toward it would be both for the offense to pass more often and the defense to defend the pass more often as a response. But that is something different than saying that the offense "should pass more." To argue that, you'd have to demonstrate that the Nash equilibrium returns a higher total value than the current state. If the defense did not respond at all to the offensive change in strategy, then obviously the ideal strategy would be to pass 100% of the time. But guessing that the defense would change - thereby altering the frequency-dependent matrix values and driving closer to the Nash eq. - you really need to know whether the current state is better or worse than the Nash eq. *for the offense* before recommending that they change strategies. This violates some "rational acting" tenets of game theory, but if you know that your opponent is behaving inefficiently and is unlikely to change unless you draw attention to that fact, then staying pat may be the better utility move.
Again, without actual data for frequency dependent utility returns - which would necessitate WAY more data points - it's hard to say exactly what the proper course is. But the fact that the offense is not maximally exploiting the current defensive strategy does not entail that one should definitely maximally exploit it if you know that would cause the opponent to behave more rationally.
Please correct me if I'm wrong here - not as brushed up on my stats as I would like - but the discussion here has essentially been based on the idea that, if I had to call the next play, what play type will yield the most points.
Clearly, passing yields more yards, and in down-starved leagues (i.e. CFL) or situations (e.g. 3rd and long), passing is forced more often. However, one question I want to understand is the strategic question - over the course of the game, what has run-pass balance meant to win percentage (when quality of air attack and run attack have been accounted for - it's no sense blaming losing on a run-first philosophy if the air attack is so bad their isn't any other way - e.g. if your QB is a rookie Gabbert or so-so Henne, can you be blamed for relying on Jones-Drew?).
Again, correct me if I'm wrong, but running plays are known to be easier on the O-line (they can attack the D-line rather than simply try to resist their rush), wear out defenses faster(have many defenders not indicated their distaste for dealing with the run, especially against physical RBs? Jimmy Johnson's theory that tired men are more cowardly and therefore less likely to make a play ring very strongly here), and have increasing payoffs as the game wears on (again, if you have the evidence, please prove/disprove, but it seems on observation that runs in the 1st quarter yield fewer yards on average than 4th quarter runs)? Also, by running more, obviously time on the clock is reduced, thereby reducing the total number of plays in a game, and, at least in theory, the opponent's scoring opportunities?
To be clear - I'm not trying to argue the relative tactical value of a run vs. a pass. The pass tends to yield more per play, full stop. What I'm asking is, in the context of a full game, and accounting for relative quality of air and ground attack, what would the optimum run-pass mix look like? At least in theory, would it be possible to predict the optimum mix based on the relative quality of a given team's air and ground attacks (understanding that that ratio would probably change based on the opposing defense's characteristics)?
Addendum to above: forgive the repetition of some of the points on the benefits of the run from previous posts - but my question stands: what is the optimum run-pass ratio over an entire game? How can I use this analysis to pick a better game long strategy? Can this data be set up based on relative qualiity of air and ground attacks?
Brian:
Do you have an update of these data, and/or a disaggregation of the data? As you point out, these data are necessarily uncontrolled, and there likely is some impact of a change in balance on the expected outcomes. So, I'm wondering whether teams have maybe started passing more after 2008 so that we could see whether the outcomes changed. Alternatively, if you can isolate a sample with a significant difference in balance, we could test it that way as well.