The Probability of Responding to a Successful FG
If the defense plays conventionally, and the opponent's FG is successful, a score will be needed to win. Either a FG or TD will do. We can assume that the drive will began at or very near the offense's own 20-yard line for a couple reasons. First, the average starting field position for all drives is the 22. And second, it's very likely that, with time at a premium, the offense would prefer a touchback so that no time expires on the kickoff.
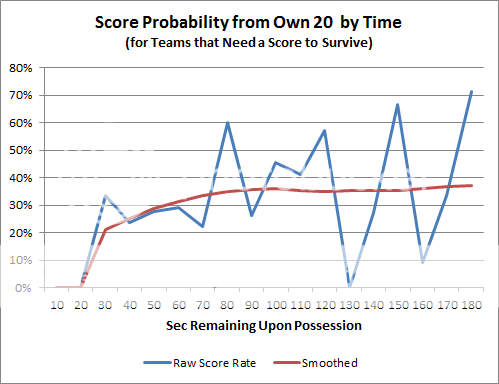
For this estimate, I looked at all game situations in which an offense needed a score to survive and had a 1st down at or very near its own 20. Success is defined as any drive that results in a TD or FG.
The blue line is the raw success rate as a function of seconds remaining at the 1st down snap. The red line is the smoothed estimate of the probability of scoring based on a local regression. Because there were several bins of data with very few cases (which caused the large noisy swings in the raw averages), I used a regression method that weighted each case by how often it appeared. In other words, if there were 10 cases where a team gained possession with around 50 seconds to play and 20 with around 60 seconds to play, the regression weighted each bin of cases proportionately.
The probability of success drops precipitously under 30 seconds to play. That appears to be the very least amount of time for a team to get into FG range from a team's own 20. But time in excess of 30 seconds is only marginally more valuable as time remaining increases.
The Probability of Responding to a TD
In this case, the offense now needs a TD of its own. Like the situation that requires a response to a FG, the team now on offense is assumed to gain possession at or very near its own 20-yard line. The preceding TD play was estimated to consume six seconds.
For this estimate I looked at all endgame situations in which the offense needed a TD to survive and had a 1st down very near its own 20. The graph below plots the success rate by time remaining. As mentioned previously, timeouts remaining for the offense do not have a measurable effect. The jagged blue line is the raw data, and the red line is the smoothed estimate.
Without the possibility of a FG, the curve appears smoother than the probability of either a TD or FG, at least according to the regression. I intuitively suspect that the true probability is closer to initial steepness that the raw numbers indicate, but for now I'm leaving the regression as is. It's another factor I'd be willing to revisit.
Comparing the two charts (FG or TD needed vs. TD needed) suggests that teams play differently, and perhaps irrationally, based on the score situation. When time is not too pressing (with about 2 minutes or slightly more to play), offenses that need a TD appear slightly more likely to be successful than those that only need a FG. I suspect this is due to the illusion of FG "range" as well as risk-reward balance for both the offense and defense.
Next, the fifth and final part of this series will put everything together and present the results.










Regarding the TD v FG probability, I'm guessing that's the effect of playing 4-down offense against a prevent defense.
There's a fairly common theme in football that a tactic designed to be 'safe' (e.g. prevent defense, punting on 4th down etc) actually costs teams wins. Part of me thinks it's because these tactics were designed in an era when moving the ball was significantly harder so they probably did make sense back then.
Yep. I think it's a function of time as well. Teams bet on getting the ball back after punting when it's actually very unlikely.
Of course "playing safe" will sometimes cost teams a win. It is not a guarantee. I suspect there is an enormous confirmation bias in the "well known" idea that prevent defenses cost wins.
The question is, does playing it safe cost a win more than the typical defense, and does it cost more wins than an aggressive defense?